GIỚI THIỆU VỀ PHƯƠNG TRÌNH VI PHÂN .
Chương 6 -
PHẦN 1 .
-Bài toán Sturm - Liouville
-Các hàm đặc biệt .
Loạt bài sau đây giới thiệu về phương trình vi phân một cách tổng quan , các khái niệm cơ bản và phương pháp giải được trình bày tinh giản dễ hiểu . Bạn đọc có thể sử dụng các phần mềm hoặc công cụ online trích dẫn chi tiết trong bài viết này để hỗ trợ cho việc học tập và nghiên cứu . Ngoài ra tác giả cũng sẽ đề cập đến những ví dụ minh họa cụ thể , các mô hình thực tế có ứng dụng trong lĩnh vực phương trình vi phân .
Trần hồng Cơ .
19/10/2013 .
****************************************************************************

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
1. Bài toán giá trị biên .
1.1 Các bài toán giá trị biên cấp 2 cơ bản .
+Để đơn giản hóa vấn đề chúng ta xét phương trình vi phân cấp 2 với các điều kiện như sau
Ràng buộc cho những phương trình vi phân trên đây đặt tại các điểm được gọi là giá trị biên hay điều kiện biên của phương trình . Bài toán tìm nghiệm của phương trình vi phân cấp 2 với các điều kiện biên được gọi là bài toán giá trị biên cấp 2 .
Phân loại .
+Điều kiện biên tại x = x0 gọi là chuẩn <=>
ay(x0) + by'(x0) = c , với a , b , c là các hằng số không đồng thời bằng 0 .
+Điều kiện biên tại x = x0 gọi là giới nội <=>
|y(x0)| < $\infty$ hay $\lim_{x\rightarrow xo}\left | y(x) \right |< \infty$
+Điều kiện biên tại x = x0 gọi là tuần hoàn <=> có một giá trị x1 khác với x0 sao cho
y(x0) = y(x1) và y'(x1) = y'(x1)
1.2 Kiến thức bổ sung .
+Sau đây là phần bổ sung về đại số tuyến tính trước khi đi vào chi tiết bài toán Sturm - Liouville .
a. Số phức .
Số phức z = x + iy , x = Re(z) : phần thực của z , y = Im(z) phần ảo của z .
Modulo của z , ký hiệu là | z |
$\left | z \right |=\sqrt{x^2+y^2}$
Số phức liên hợp z* = x - iy
Ta có $zz^{*}=\left | z \right |^2=x^2+y^2$
b. Vector trong Rn - Ma trận thực đối xứng .
Vector trong Rn có dạng u = (u1,u2,...,un) với uj ( j =1,2..,n ) là số thực .
Chuẩn của u , ký hiệu || u ||
$\left \| u \right \|=\sqrt{u_{1}^2+u_{2}^2+...+u_{n}^2}$
Tích vô hướng của u và v , ký hiệu u.v
u.v = u1v1 + u2v2 +...+ unvn
Ta có $u.u=\left \| u \right \|^2$ .
Hai vector u , v gọi là trực giao <=> u.v = 0 ( tích vô hướng = 0 ) .
+Ma trận Anxn = [ aij ] với aij ( i, j =1,2..,n ) là số thực gọi là ma trận đối xứng <=> aij = aji ( i, j =1,2..,n ) .
Hay ta còn viết $A=A^{T}$
Trị đặc trưng m của ma trận A là nghiệm của phương trình đặc trưng det( A - mI ) = 0 .
Vector u gọi là vector đặc trưng tương ứng với trị đặc trưng m của ma trận A <=> Au = mu .
+Tính chất của ma trận đối xứng .
Cho A là ma trận đối xứng , khi đó
(i) Các trị đặc trưng của A là thực .
(ii) Tồn tại cơ sở trực giao của Rn gồm các vector đặc trưng của A .
c. Vector trong Cn - Ma trận phức tự-liên hợp .
Vector trong Cn có dạng u = (u1,u2,...,un) với uj ( j =1,2..,n ) là số phức .
Chuẩn của u , ký hiệu || u ||
$\left \| u \right \|=\sqrt{|u_{1}|^2+|u_{2}|^2+...+|u_{n}|^2}$
Tích trong của u và v , ký hiệu $\left \langle u|v \right \rangle$
$\left \langle u|v \right \rangle=\sum_{j=1}^{n}u_{j}^{*}v_{j}$
Trong đó uj* là phức liên hợp của uj . Hai vector u , v gọi là trực giao <=> $\left \langle u|v \right \rangle$ = 0 ( Tích trong = 0 ).
+Tính chất của tích trong .
Giả sử a , b là hai số phức , u và v là vector thuộc Cn .
$\left \langle u|v \right \rangle=\left \langle v|u \right \rangle^{*}$
$\left \langle u|av+bw \right \rangle=a\left \langle u|v \right \rangle+b\left \langle u|w \right \rangle$
$\left \langle av+bw|u \right \rangle=a^{*}\left \langle v|u \right \rangle+b^{*}\left \langle w|u \right \rangle$
$\left \langle u|u \right \rangle=\left \| u \right \|$
+Ma trận Anxn = [ aij ] với aij ( i, j =1,2..,n ) là số phức , $A^{\dagger }$ gọi là ma trận liên hợp <=> $A^{\dagger }=\left ( A^{*} \right )^{T}$ .
Ma trận A được gọi là tự liên hợp ( hay Hermite )<=> $A=A^{\dagger }$
Ví dụ . Tìm ma trận liên hợp
Ví dụ . Xét tính tự liên hợp của ma trận
+Tính chất của ma trận tự liên hợp ( Hermite ) .
-Ma trận A tự liên hợp thì A phải là ma trận vuông .
-Ma trận tự liên hợp có các phần tử trên đường chéo chính là thực .
-Ma trận tự liên hợp có các trị riêng là thực và có n vector riêng độc lập tuyến tính .
-Ma trận A tự liên hợp thì tồn tại một cơ sở trực giao trong Cn gồm các vector đặc trưng của A .
-Ma trận vuông A có các phần tử là thực và $A=A^{\dagger }$ thì A là ma trận thực - đối xứng .
d. Khai triển một vector trong Cn theo cơ sở trực chuẩn .
Mọi vector trong Cn có dạng u = (u1,u2,...,un) với uj ( j =1,2..,n ) là số phức đều có thể khai triển thành một tổ hợp tuyến tính của các vector cơ sở trực giao { bk , k = 1,2,...,n } .
$u=\sum_{k=1}^{n}C_k.\mathbf{b}_k,C_k\in \textbf{C}$
Các hệ số Ck được tính bởi
$C_k=\frac{\left \langle \mathbf{b}_{k}|u \right \rangle}{\left \|\mathbf{b}_{k} \right \|^{2}} , k=1,2,...,n$
+Cơ sở { bk , k = 1,2,...,n } được gọi là trực chuẩn khi $\left \| \mathbf{b}_{k} \right \|=1$ . Từ cơ sở trực giao { bk , k = 1,2,...,n } ta có thể xây dựng cơ sở trực chuẩn bằng cách đặt $\mathbf{e}_k=\frac{\mathbf{b}_k}{\left \| \mathbf{b}_k \right \|}$
Khi đó { ek , k = 1,2,...,n } sẽ là cơ sở trực chuẩn .
e. Tích trong và ma trận liên hợp .
+Nhắc lại về ma trận chuyển vị và ma trận liên hợp .
Ta có các công thức sau
$(A^{T})^{T}=A , (AB)^{T}=B^{T}A^{T},(A^{*})^{*}=A , (AB)^{*}=A^{*}B^{*}$
$A^{\dagger }=\left ( A^{*} \right )^{T}$
+Đối với ma trận liên hợp .
$(A^{\dagger})^{\dagger}=A , (AB)^{\dagger }=B^{\dagger}A^{\dagger}$
Xét 2 vector u và v trong Cn , theo định nghĩa của liên hợp ta có
$u^{\dagger }=\left ( u^{*} \right )^{T}$
Tích trong và tích ma trận liên hệ với nhau
$u^{\dagger}v=[u_1^{*},u_2^{*},u_3^{*},..,u_n^{*}]\begin{bmatrix} v_1\\v_2\\v_3\\...\\v_n\end{bmatrix}=\sum_{j=1}^{n}u_j^{*}v_j$
Mặt khác , $\left \langle u|v \right \rangle=\sum_{j=1}^{n}u_{j}^{*}v_{j}$
Nên $u^{\dagger}v=\left \langle u|v \right \rangle$
+Định lý .
Cho ma trận phức Anxn = [ aij ] , $A^{\dagger }$ là ma trận liên hợp tương ứng của A .
(i) $\left \langle Au|v \right \rangle=\left \langle u|A^{\dagger} v \right \rangle$
(ii) $A^{\dagger}=B\Leftrightarrow \left \langle Au|v \right \rangle=\left \langle u|B v \right \rangle$
(iii) $A^{\dagger}=A\Leftrightarrow\left \langle Au|v \right \rangle=\left \langle u|A v \right \rangle$
*Sơ lược tiểu sử .
| Charles Hermite | |
|---|---|

Charles Hermite circa 1887
| |
| Sinh | December 24, 1822 Dieuze, Moselle |
| Mất | January 14, 1901 (aged 78) Paris |
| Quốc tịch | French |
| Lĩnh vực | Mathematics |
| Institutions | École Polytechnique Sorbonne |
| Alma mater | Collège Henri IV, Sorbonne Collège Louis-le-Grand,Sorbonne |
| Doctoral students | Léon Charve Henri Padé Mihailo Petrović Henri Poincaré Thomas Stieltjes Jules Tannery |
| Known for | Proof that e is transcendental Hermitian adjoint Hermitian form Hermitian function Hermitian matrix Hermitian metric Hermitian operator Hermite polynomials Hermitian transpose Hermitian wavelet |
2.1 Tổng quan .
+Trong lĩnh vực toán ứng dụng , phương trình cổ điển Sturm-Liouville - được đặt tên theo hai nhà toán học Jacques Charles François Sturm (1803-1855) và Joseph Liouville (1809-1882) - là phương trình vi phân tuyến tính bậc hai có dạng (1)
+Trường hợp đơn giản nhất là tất cả các hàm số đều liên tục trên đoạn [ a, b ] , và P(x) có đạo hàm liên tục . Khi đó "y(x)" được gọi là nghiệm nếu nó khả vi liên tục trên khoảng (a, b) và thỏa mãn phương trình ( 1 ) tại tất cả các điểm thuộc (a, b) . Ngoài ra, ẩn hàm y(x) thường được yêu cầu phải đáp ứng một số điều kiện biên tại a và b. Hàm R(x) , được gọi là hàm " trọng lượng " hay hàm " mật độ ".
+Giá trị m không được quy định trong phương trình, việc tìm kiếm các giá trị của m để tồn tại một nghiệm không tầm thường của (1) thỏa mãn các điều kiện biên là một phần của bài toán Sturm - Liouville ( S-L ) . Giá trị m như vậy khi chúng tồn tại , được gọi là các giá trị riêng của bài toán biên được xác định bởi (1) và tập hợp quy định của điều kiện biên. Các nghiệm tương ứng đối với m gọi là hàm riêng của bài toán này .
+Dưới các giả thiết bình thường về các hàm số P(x) , Q(x) và R(x) ở trên , sẽ dẫn đến việc tạo ra một toán tử vi phân Hermite trong không gian hàm nào đó được xác định bởi các điều kiện biên . Kết quả lý thuyết về sự tồn tại và dáng điệu tiệm cận của các giá trị riêng , lý thuyết định tính tương ứng về các hàm riêng và tính đầy đủ của chúng trong một không gian hàm phù hợp được gọi là lý thuyết Sturm - Liouville . Lý thuyết này có vai trò rất quan trọng trong toán ứng dụng , khi mà bài toán S -L xảy ra rất phổ biến , đặc biệt với các phương trình vi phân đạo hàm riêng tuyến tính khả tách .
+Bài toán (S-L) Sturm-Liouville được gọi là chuẩn nếu P(x), R(x)> 0 , các hàm P(x), P'(x), Q(x) và R(x) là các hàm liên tục trong đoạn
[a, b] có các điều kiện biên được tách như trong (1) .
2.2 Một số tính chất của hàm riêng .
Dưới các giả thiết bài toán chuẩn S-L , nguyên lý chính của lý thuyết Sturm-Liouville phát biểu rằng:
1. Các giá trị riêng m1, m2, m3, ... của bài toán chuẩn Sturm-Liouville (1) là thực và có thể được sắp thứ tự như sau
m1 < m2 < ... < mn < ...
2. Tương ứng với mỗi giá trị đặc trưng mn là một hàm riêng yn(x) duy nhất có đúng (n - 1) không điểm trên khoảng (a, b) . Các hàm riêng yn(x) được gọi là nghiệm cơ sở thứ -n thỏa mãn bài toán chuẩn Sturm-Liouville (1)
3. Các hàm riêng {yn(x) , n = 1,2,...} chuẩn hóa tạo thành một cơ sở trực chuẩn trong không gian Hilbert L2{[a,b],R(x)} thỏa mãn
Với hàm f(x) liên tục từng khúc ta có thể biểu diễn qua cơ sở trực chuẩn {yn(x) , n = 1,2,...} như sau
Tính đầy đủ cho phép biểu diễn một hàm từng khúc thành chuỗi các hàm riêng và tính trực chuẩn là để bảo đảm sự duy nhất và compact .
2.3 Các dạng đặc biệt của phương trình Sturm - Liouville .
a. Các hàm - đa thức dẫn xuất .
+ Phương trình vi phân Bessel là trường hợp đặc biệt của Sturm-Liouville - với
Nghiệm của phương trình vi phân Bessel gọi là hàm Bessel loại 1 , Jn(x) xác định trên $(0,+\infty )$ .
+ Phương trình vi phân Chebyshev là trường hợp đặc biệt của Sturm-Liouville - với
Nghiệm của phương trình vi phân Chebyshev gọi là đa thức Chebyshev , Tn(x) xác định trên (-1,1) .
+ Phương trình vi phân Laguerre là trường hợp đặc biệt của Sturm-Liouville - với
Nghiệm của phương trình vi phân Laguerre gọi là đa thức Laguerre , Ln(x) xác định trên (0,+00) .
Nghiệm của phương trình vi phân Legendre gọi là đa thức Legendre , Pn(x) xác định trên [-1,1] .
b. Thừa số tích phân IF .
+ Đối với phương trình vi phân cấp 2 , khi nhân hai vế phương trình cho thừa số tích phân ta cũng quy về trường hợp đặc biệt của phương trình Sturm-Liouville .
Xét phương trình vi phân cấp 2 tổng quát
| Jacques Charles François Sturm | |
|---|---|

Jacques Charles François Sturm
| |
| Sinh | 29, tháng 9 , 1803 Geneva |
| Mất | 15, tháng 12 1855 (aged 52) Paris |
| Quốc tịch | Pháp |
| Lĩnh vực | Toán học |
| Institutions | École Polytechnique |
| Công trình | Sturm–Liouville theory Sturm's theorem Speed of sound |
| Giải thưởng | Légion d'Honneur (1837) Copley Medal (1840) |
| Joseph Liouville | |
|---|---|

Joseph Liouville
| |
| Sinh | 24 , tháng 3 , 1809 Saint-Omer |
| Mất | 8 , tháng 9 , 1882 (73 tuổi ) Paris |
| Quốc tịch | Pháp |
| Lĩnh vực | Mathematics |
| Alma mater | École Polytechnique |
| Doctoral advisor | Siméon Poisson Louis Jacques Thénard |
| Doctoral students | Eugène Charles Catalan |
Trần hồng Cơ .
26/10/2013 .

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
-------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
Pure mathematics is, in its way, the poetry of logical ideas.
Albert Einstein .







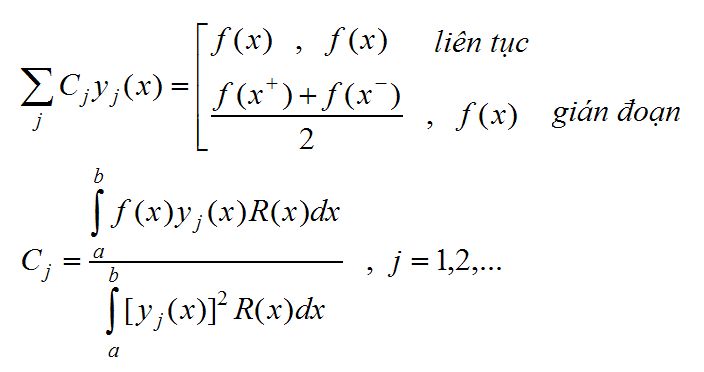










Không có nhận xét nào:
Đăng nhận xét
Cám ơn lời bình luận của các bạn .
Tôi sẽ xem và trả lời ngay khi có thể .
Thank you for your comments.
I will review and respond to these issues as soon as possible.
Trần hồng Cơ .
Co.H.Tran
MMPC-VN
cohtran@mail.com