
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
Đây
là tài liệu môn Mathematics dành cho sinh viên chuyên ngành Quản
trị kinh doanh của chương trình Du học tại chỗ - Liên kết đào tạo với
Đại học Hoa kỳ , tác giả đã trực tiếp biên soạn và giảng dạy các năm
2008-2010 . ( Xem đề cương chi tiết tại http://cohtran.yolasite.com/semester-courses.php )
Bản
gốc giáo trình này bằng tiếng Anh , được dịch và chỉnh lý sang Việt ngữ
với tựa đề TOÁN ĐƠN GIẢN - TOÁN HỌC THỰC HÀNH với ý định rõ ràng : đó là cung cấp cho người
đọc những khái niệm Toán học cùng các ứng dụng trong thực tế .
Như
tên gọi của nó , thật hết sức đơn giản khi làm việc với những định
nghĩa , định lý , hệ quả và đặc biệt là việc vận dụng linh hoạt các nội
dung này vào những hoạt động khoa học-kinh tế -xã hội , nhận biết được
các lợi ích cũng như những dự báo có tính chính xác tương đối cao .
Rất mong nhận được nhiều đóng góp tích cực từ người đọc để bản thảo này được hoàn thiện hơn .
Xin liên lạc với tác giả qua e-mail : cohtran@mail.com
Trần hồng Cơ ,
Ngày 19/06/2012 .
COURSE SYLLABUS
MATHEMATICS
Lecturer : MSc Math-Mech
TRAN HONG CO .
Introduction
The
goal of this course is to expose students to topics in Mathematics that are
often used in scientific approaches especially in economic and business
management . The mathematic course contains many problems from the basic to the
advanced, to supply student with a wide
range of abilities and interests. Beside some of the examples are simply
designed to build skills, every effort has been made to generalize problems, so
that students can see common uses and practical applications of the mathematics
they are studying, and appreciate the power of mathematics. We hope that
students will be able to seize the essence of all the matters and also make use
of mathematical concepts to the realities .
Objectives
There are three objectives :
1 .To introduce the basic concepts in mathematics :
sets , counting and logic . From the such essentials , the students would be
provided knowledge to access data with combinatorics , probability and
financial tools .
2 . Considering the operations
and applications of matrices . The
students would be communicated key concepts in linear algebra and usefulness of
matrices for solving the optimization problem and prediction by Markov’s chains
.
3 . To provide the concepts in calculus and
applications to the students briefly but completely including limitation ,
differentiation and integration .
Materials
Students can refer to materials as following
-Mathematics – A practical course , CoHongTran , 2008
-Mathematics for the international student , Paul Urban ,
Haese-Harris
Publications , 2004 .
-Calculus I , Paul Dawkins , 2007 . -Business Calculus
Demystify , Rhonda HuettenMueller , Mc Graw-
Hill , 2006 .
-Mathematics –A practical Odyssey , David B. Johnson ,
Thompson-Brooks/Cole , 2005 .
Contents
Mathematics is a 16-week course , including 7 chapters , 5
home assignments , a midterm and final test .
Chapter 1 . LOGIC , SETS AND COUNTING
1.1 SETS – BINARY OPERATIONS
1.2 SYMBOLIC LOGIC – BICONDITIONAL
1.3 COUNTING - COMBINATORIAL LOGIC
Chapter 2 . PROBABILITY , STATISTICS AND FINANCE .
2.1 PROBABILITY - COMBINATORICS
–EXPECTED VALUE
2. 2 STATISTICS , LINEAR REGRESSION
2. 3 FINANCE
Chapter 3 . GEOMETRY
3.1 GEOMETRICAL FORMULAS
3.2 POLYGON GEOMETRY
3.3 SPACE SOLID GEOMETRY
3.4 2D AND 3D COORDINATE SYSTEMS
3.5 TRIGONOMETRY
3.6 CONIC
Chapter 4 . LINEAR ALGEBRA
4.1 MATRICES – BASIC OPERATIONS
4.2 INVERSE MATRICES – MATRIX EQUATIONS
4.3 SYSTEMS OF LINEAR EQUATIONS WITH NON-UNIQUE SOLUTIONS
4.4 SYSTEMS OF LINEAR INEQUALITIES
4.5 LINEAR PROGRAMMING , GRAPHICAL METHODS
4.6 MARKOV CHAINS
CHAPTER 5 . EXPONENTIAL AND LOGARITHM
5.1 EXPONENTIAL FUNCTIONS
5.2 LOGARITHMIC FUNCTIONS
5.3 SOLVING EXPONENTIAL EQUATIONS – LOGARITHMIC EQUATIONS
5.4 EXPONENTIAL AND LOGARITHMIC MODELS
CHAPTER 6 . CALCULUS
6.1 SEQUENCES - DISCRETE FUNCTIONS
6.2 SERIES
6.3 LIMITS OF FUNTIONS
6.4 THE DERIVATIVE
6.5 THE INTEGRATION
CHAPTER 7 . APPLICATIONS OF DERIVATIVES AND INTEGRATIONS
7.1 APPLICATIONS OF DERIVATIVES
7.2 APPLICATIONS OF DERIVATIVES ( cont )
7.3 APPLICATIONS OF INTEGRATIONS
7.4 APPLICATIONS OF INTEGRATIONS (cont)
Assignments
There are 5 home assignments based on the topics in chapters
above .
HOME ASSIGNMENT 1
1. LOGIC , SET , COUNTING
2. PROBABILITY , STATISTICS
HOME ASSIGNMENT 2
1. FINANCE
2 .GEOMETRY
2 .GEOMETRY
HOME ASSIGNMENT 3
1. GEOMETRY
2. LINEAR ALGEBRA
HOME ASSIGNMENT 4
1. EXPONENTIAL AND LOGARITHM
2. CALCULUS
HOME ASSIGNMENT 5
1. LIMITS
2 . DERIVATIVE
3. INTEGRATION
Examinations
The midterm and final test are open-book examinations and 1
½ hours long both . The midterm covers chapters 1 – 4 , and final covers
chapters 5 – 7 .
Grading
The final grade will be determined as follows
TOTAL HOME ASSIGNS SCORES 30%
MIDTERM SCORES 35%
FINAL SCORES 35%
MIDTERM SCORES 35%
FINAL SCORES 35%
FINAL
|
||
SCORES
|
GRADES
|
|
0
|
F
|
|
60
|
C-
|
|
64
|
C
|
|
71
|
C+
|
|
75
|
B-
|
|
79
|
B
|
|
86
|
B+
|
|
90
|
A-
|
|
94
|
A
|
|
-----------------------------------------------------------------------------------------------------------
Chương 1 . LOGIC , TẬP HỢP VÀ
PHÉP ĐẾM .
Bài giảng
1.1
TẬP HỢP – PHÉP TOÁN TẬP HỢP .
Chủ đề
- Tập hợp và tập hợp con .
- Phép toán tập hợp .
- Luật De Morgan .
Ứng dụng
-Xác định bản số tập hợp .
Khái niệm cơ bản
* Phép toán tập hợp ( Hợp , Giao , Hiệu – Phần bù )
.
1.
Tập hợp – tập hợp con .
- Một tập hợp là một bộ sưu tập các đối tượng hoặc sự vật có cùng tính
chất . Những đối tượng hoặc sự vật đó gọi là phần tử của tập hợp .
Ví dụ A = { a , b , c , 1 , 2
, x , y }
- Bản số của tập hợp A là số phần tử của A ký hiệu là card(A) hoặc
n(A) .
Ví dụ A = { a , b , c , 1 , 2
, x , y } , n(A)
= 7
- Tập hợp có thể được biểu
diễn bởi giản đồ Venn như sau ( Venn
diagram )

Ví dụ . * Lập đội điền kinh .
Có 148 sinh viên tham gia tập luyện thể dục thể thao trong đó có 76 người thích chạy bộ , 112 người thích nhảy sào và 28 người không thích cả hai bộ môn này . Hỏi số sinh viên vừa thích cả hai môn này là bao nhiêu người để từ đó lập ra một đội tuyển thi đấu điền kinh .
Lời giải .
Gọi tổng số sinh viên tập luyện thể thao là n(T) = 148 người
Số sinh viên thích chạy bộ là n(B) = 76 người
Số sinh viên thích nhảy sào là n(S) = 112 người
Số sinh viên không thích chạy bộ và nhảy sào là n(~BUS) = 28 người
Tập hợp những nsinh viên thích cả hai môn ký hiệu là B^S .
Vậy số người thích chạy bộ hoặc nhảy sào hoặc cả hai môn này là
n(BUS) = n(T) \ n(~BUS) = 148 - 28 = 120 ( người )
n(BUS) = n(B) + n(S) - n(B^S)
hay 120 = 76 + 112 - n(B^S)
Khi đó n(B^S) = 76 + 112 - 120 = 68 ( người )
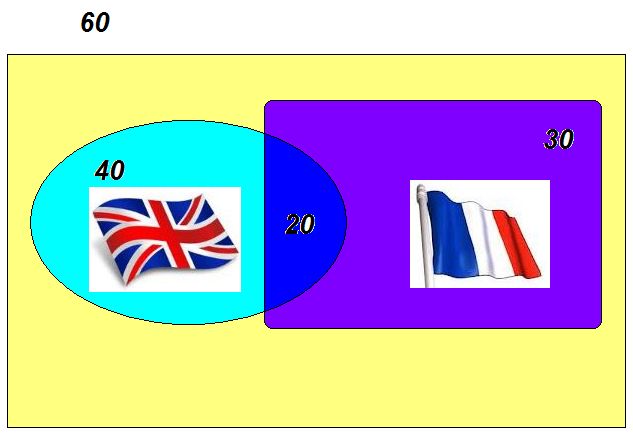
Ví dụ . * Lựa chọn ngoại ngữ .
Khoa quản trị có 60 sinh viên trong đó có 40 chọn ngoại ngữ Anh , 30 chọn ngoại ngữ Pháp và 20 người chọn cả hai bộ môn này .
Hỏi số sinh viên
a. Chỉ chọn ngoại ngữ Anh .
b. Chỉ chọn ngoại ngữ Pháp .
c. Không chọn cả hai ngoại ngữ Anh và Pháp .
d. Chọn một trong hai hoặc cả hai ngoại ngữ .
Lời giải .
Lời giải .
Gọi tổng số sinh viên của khoa là n(K) = 60
Số sinh viên chọn Anh văn là n(A) = 40 người
Số sinh viên chọn Pháp văn là n(P) = 30 người
Số sinh viên chọn cả hai Anh văn và Pháp văn là n(A^P) = 20 người .
a. Như vậy số sinh viên chỉ chọn Anh văn là : n(A~P) = 40 - 20 = 20 (người)
b. Số sinh viên chỉ chọn Pháp văn là : n(P~A) = 30 - 20 = 10 (người)
Như vậy n(AUP) = n(A\P) + n(P) = ( 40 - 20 ) + 30 = 50 (người)
c. Số sinh viên không chọn cả hai ngoại ngữ là
n(~A^~P) = n(K) - n(AUP) = 60 - 50 = 10 ( người)
d. Số sinh viên chọn một trong hai hoặc cả hai ngoại ngữ là
n(AUP) = 50 (người)
*************************************************
Trần hồng Cơ
20/6/2012 
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
1.2 LOGIC HÌNH THỨC – SONG ĐIỀU KIỆN .
Chủ đề
- Tập hợp và tập hợp con .
- Quan hệ logic .
- Luật De Morgan .
Ứng dụng
-
Khái niệm cơ bản
* Phép toán tập hợp ( Hợp , Giao , Hiệu – Phần bù )
.
1. LOGIC HÌNH THỨC .
Bảng so sánh các thành phần
và ký hiệu dùng trong lý thuyết
tập hợp và logic mệnh đề .
Ví dụ . Lập
bảng chân trị của biểu diễn hình thức .
Lời giải
Ví dụ . Chứng tỏ rằng
là mệnh đề lặp thừa tautology . ( i.e luôn luôn đúng )
Hệ thống logic mệnh đề theo trường phái khắc kỷ được trình bày dưới dạng lý thuyết diễn dịch với 5 qui tắc diễn dịch cơ bản được coi như những tiên đề sau :
+++++++++++++++++++++++++++++++++++++++++++++++
(1)Nếu có A thì có B, mà có A vậy có B.
( A =
> B )
(2)Nếu có A thì có B, mà không có B vậy không có A.
( A = > B < = > ~B => ~A )
( A = > B < = > ~B => ~A )
(3)Không có đồng thời A và B, mà có A vậy không có B.
( ~ ( A ^ B ) ^ A => ~B )
( ~ ( A ^ B ) ^ A => ~B )
(4)Hoặc A hoặc B, mà có A vậy không có B.
[ ( ~A ^ B ) V ( ~B ^ A ) ]^ A => ~B
(5)Hoặc A hoặc B, mà không có B vậy có A.
[ (~A ^ B ) V ( ~B ^ A ) ] ^ ~B => A
+++++++++++++++++++++++++++++++++++++++++++++++
*************************************************
Trần hồng Cơ
20/6/2012 
This work is licensed under a
Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
-------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
Pure mathematics is, in its way, the poetry of logical ideas.
Albert Einstein .
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
TOÁN THỰC HÀNH CHƯƠNG 1 . 1.3
1.3 PHÉP ĐẾM - LOGIC TỔ HỢP .
Chủ đề
- Cơ sở phép đếm Fundamental of counting .
- Logic tổ hợp .
Ứng dụng
- Tính toán với phép đếm .
Khái niệm cơ bản
* Logic tổ hợp ( Giai thừa -Factorial , Chỉnh hợp-Permutation , Tổ hợp - Combination ) .
1. NGUYÊN LÝ CƠ SỞ CỦA PHÉP ĐẾM - FUNDAMENTAL PRINCIPAL OF COUNTING
Phép cộng - Addition Rule
Giả sử rằng ta phải giải quyết một việc gì đó với 2 phương án A hoặc B và có m , n cách quyết định tương ứng cho các phương án đó , khi đó ta có thể chọn được m+n cách để đạt được kết quả .
Ví dụ . Có mấy cách đi vào trường học nếu có 5 cổng chính và 3 cổng phụ .
Lời giải
Phép nhân - Multiplication Rule
Giả sử rằng ta phải giải quyết một việc gì đó với 2 phương án A và B và có m , n cách quyết định tương ứng cho các phương án đó , khi đó ta có thể chọn được m . n cách để đạt được kết quả .
Ví dụ . Một số serial gồm 2 phụ âm theo sau bởi 3 chữ số khác 0 và tiếp theo là 1 nguyên âm { A , E , I , O , U } . Hãy xác định xem có bao nhiêu số serial được tạo thành biết
a. Chữ và số không được lập lại trong một serial .
b. Chữ và số có thể được lập lại trong một serial .
Lời giải .
a. Mẫu của một số serial với “ Chữ và số không được lập lại ” có dạng như sau
b. Mẫu của một số serial với “ Chữ và số có thể được lập lại ” có dạng như sau
2. LOGIC TỔ HỢP - COMBINATORIAL LOGIC
GIAI THỪA - FACTORIAL
Giai thừa của số nguyên dương n
(read n factorial) kí hiệu n ! xác định bởi
n ! = n (n − 1) (n − 2) . . .3 2 1 .
Ví dụ . 4! = 4 .3. 2. 1 = 24. Quy ước 0! = 1.
Từ các chữ số { 1,2,3,4,5,6 } có thể lập được bao nhiêu số gồm 6 chữ số khác nhau .
Lời giải .
CHỈNH HỢP - PERMUTATION
Chỉnh hợp - Permutation : là một sự sắp xếp có thứ tự gồm một số đặc biệt các phần tử được chọn từ 1 tập hợp . Số các chỉnh hợp gồm r phần tử từ n phần tử là n!/(n-r)! thường viết [n]P[r]
hay ^(n )P[r].
TỔ HỢP - COMBINATION
Tổ hợp – Combination : là một sự sắp xếp không có thứ tự gồm một số đặc biệt các phần tử được chọn từ 1 tập hợp . Số các tổ hợp gồm r phần tử từ n phần tử là n!/ [ r!(n-r)!] thường viết [n]C[r]
hay ^(n )C[r].
*************************************************
Trần hồng Cơ
28/9/2012
This work is licensed under a
-------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
Pure mathematics is, in its way, the poetry of logical ideas.
Albert Einstein .
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
TOÁN THỰC HÀNH CHƯƠNG 2 . 2.1
Chương 2 . XÁC SUẤT , THỐNG KÊ VÀ CÁC BÀI TOÁN ỨNG DỤNG .
Bài giảng
2.1 XÁC SUẤT ( PROBABILITY ) - ĐẠI LƯỢNG TỔ HỢP ( COMBINATORICS ) - GIÁ TRỊ KỲ VỌNG ( EXPECTED VALUE )
Chủ đề
- Khái niệm cơ bản về xác suất .
- Luật xác suất .
- Đại lượng tổ hợp , giá trị kỳ vọng .
- Xác suất có điều kiện .
Ứng dụng
- Tung súc sắc .
- Khuyết tật trong sản xuất .
- Xổ số .
- Chơi bài .
- Tung đồng xu .
Khái niệm cơ bản
* Khaí niệm ( Thực nghiệm - Experiment – Biến cố – Luật số lớn - Law of large number ) .
* Luật xác suất ( Biến cố không liên quan - Mutually exclusive events )
* Đại lượng tổ hợp - Combinatorics ( Giá trị kỳ vọng -Expected value )
* Xác suất có điều kiện - Conditional probability ( Luật nhân xác suất -Product rule –Biến cố phụ thuộc và biến cố độc lập -Dependent and independent events – Sơ đồ cây - Tree diagram)
++++++++++++++++++++++++++++++++++++++++++++++++++++++++
1. Khái niệm cơ bản về xác suất .
* Thực nghiệm : là quá trình thu được từ một sự quan sát hiện tượng nào đó .
* Không gian mẫu - Sample space : kí hiệu S gồm các thu hoạch khả dĩ của thực nghiệm .
* Biến cố : là tập con E của không gian mẫu S .
Ví dụ .
Thực nghiệm ( experiment ) tung súc sắc .
Thu hoạch khả dĩ ( possible outcomes ) của con súc sắc đơn là các nút 1 , 2 , 3 , 4 , 5 , 6 .
Không gian mẫu ( sample space ) là S = {1 , 2 , 3 , 4 , 5 , 6 }
Một số các biến cố khả dĩ như sau :
E1 = {3} “ xuất hiện nút 3 ”
E2 = {2,4,6} “ xuất hiện các nút chẵn ”
E3 = {1,3,5} “xuất hiện các nút lẻ ”
…
Xác suất của biến cố - Probability of an event
Ví dụ . Tung con súc sắc đồng chất . Tìm :
a. Xác suất xẩy ra nút 5 .
b. Xác suất xẩy ra nút nhỏ hơn 5 .
c. Xác suất xẩy ra nút lớn hơn 4 .
Lời giải .
a. Thực nghiệm ( experiment ) tung súc sắc .
Thu hoạch khả dĩ ( possible outcomes ) của con súc sắc đơn là các nút 1 , 2 , 3 , 4 , 5 , 6 .
Không gian mẫu ( sample space ) S = {1 , 2 , 3 , 4 , 5 , 6 } ; n(S) = 6
Nếu thực nghiệm được lập lại rất nhiều lần thì tần suất tương đối của một thu hoạch có xu hướng tiến dần về xác suất của thu hoạch đó .
2. Luật xác suất .
Luật xác suất 1
Hai biến cố không thể xẩy ra đồng thời được gọi là biến cố không liên quan – nghĩa là phần giao của 2 biến cố này là Æ .
Ví dụ . Tung con súc sắc đồng chất .
Gọi E là biến cố “ xuất hiện nút chẵn ” .
Gọi O là biến cố “ xuất hiện nút lẻ ” .
Gọi G3 là biến cố “ xuất hiện nút lớn hơn 3 ” .
a. E và G3 có phải là biến cố không liên quan ?
b. E và O có phải là biến cố không liên quan ?
Lời giải .
a. E = {2,4,6} ; G3 = {4,5,6} => E Ç G3 = {4,6} ¹ Æ
E và G3 không phải là biến cố không liên quan .
b. E = {2,4,6} ; O = {1,3,5} => E Ç O = Æ
E và O là biến cố không liên quan .
Luật xác suất 2
Ví dụ . Công ty E-Digital Ltd sản xuất các mặt hàng TV , DVD . Một cuộc khảo sát về các sản phẩm gần đây chỉ ra rằng có 5% lỗi khuyết tật của mặt hàng TV , 3% của DVD , và 7% lỗi ít nhất một trong hai mặt hàng này . Tìm xác suất của các sản phẩm của E-Digital trong các trường hợp :
a. Lỗi cả hai sản phẩm .
b. Không có thuộc cả hai sản phẩm .
Lời giải .
Kí hiệu P(T) là xác suất khuyết tật của sản phẩm TV .
P(D) là xác suất khuyết tật của sản phẩm DVD .
P(TUD) là xác suất khuyết tật của sản phẩm TV hoặc DVD .
P(TÇD) là xác suất khuyết tật của sản phẩm TV và DVD .
Bài toán được mô hình hóa bằng giản đồ Venn như sau
3. Các đại lượng tổ hợp ( COMBINATORICS ) - Giá trị kỳ vọng ( EXPECTED VALUE )
Liên quan giữa xác suất và các đại lượng tổ hợp .
Tìm xác suất bao gồm việc tìm số lần các thu hoạch khả dĩ của biến cố n(E) ( bản số của tập E ) và số các thu hoạch khả dĩ của không gian mẫu n (S) ( bản số của tập S ) . Ta thường dùng các định luật xác suất và các đại lượng tổ hợp như chỉnh hợp , tổ hợp … để tính số lần các thu hoạch khả dĩ này .
Ví dụ . Georgia , Texas, California và Maryland là 4 tiểu bang của Hoa Kỳ thường tổ chức các đợt xổ số 6 / 44 ; người tham gia được chọn 6 số bất kỳ từ 1 đến 44 . Nếu 6 số này khớp với 6 số được xổ từ lồng quay thì người chơi sẽ thắng giải . Hãy tìm xác suất thắng cuộc .
Lời giải .
Gọi E là biến cố thắng giải , vì chỉ có 1 giải duy nhất nên
n(E) = 1 . Chọn 6 số bất kỳ từ 1 đến 44 , không có thứ tự nên ta sẽ dùng công thức tổ hợp . Số cách chọn
Giá trị kỳ vọng - Expected Value
Giá trị kỳ vọng Ev của thực nghiệm được tính bởi
Ví dụ . Phân tích thông tin bán hàng , một thương gia tìm thấy tiền hoa hồng thu được hằng tuần có trong bảng xác suất sau . Tính kỳ vọng thu được tiền hoa hồng hằng tuần .
Dùng công thức tính kỳ vọng ta có Ev = $240 . Như vậy thương gia này có thể kỳ vọng rằng trong tương lai sẽ thu được một khoản tiền hoa hồng trung bình là $240 / tuần .
4 . Xác suất có điều kiện ( CONDITIONAL PROBABILITY ) - Luật nhân xác suất ( THE PRODUCT RULE ) - Biến cố phụ thuộc và biến cố độc lập ( DEPENDENT AND INDEPENDENT EVENTS )
* Xác suất của biến cố A với điều kiện có biến cố B kí hiệu là P(A|B) được cho bởi công thức
Ví dụ .
Trong cuộc điều tra thực nghiệm liên quan đến tác hại của thuốc lá , 600 người được hỏi ý kiến của họ về chất nicotine đối với sức khỏe . Những câu trả lời của họ được chỉ ra theo số liệu trong bảng sau
Tính xác suất của các hiện tượng
a. Câu trả lời là "có" ; Câu trả lời là "không" .
b. Câu trả lời là "có" từ một người nữ trong giới nữ ; Câu trả lời là "có" từ người nam trong giới nam .
c. Câu trả lời là "có" từ một người nữ trong số những người nói có ; Câu trả lời là "có" từ người nam trong số những người nói có .
d. Câu trả lời là "có" từ một người nữ trong toàn thể ; Câu trả lời là "có" từ người nam trong toàn thể .
Lời giải .
a.
* Xác suất câu trả lời “có ” là P(có) = n(có) / n(S) = 418/600 » 0.70 = 70%
* Xác suất câu trả lời “không” là P( không) = n(không) / n(S) = 140/600 » 0.23 = 23%
b. Câu trả lời là "có" từ một người nữ trong giới nữ ; Câu trả lời là "có" từ người nam trong giới nam .
Từ số liệu
Nữ
|
256
|
45
|
19
|
320
|
* Xác suất là “có”từ một người nữ trong giới nữ là P(có|nữ) = n(cóÇnữ) / n(nữ) = 256/320 » 0.80 = 80%
* Xác suất là “có”từ một người nam trong giới nam là P(có|nam) = n(cóÇnam) / n(nam) = 162/280 » 0.58 = 58%
162
|
95
|
23
|
280
|
Nói cách khác có 58% nam trả lời “có” và 80% nữ trả lời “có” trong cuộc khảo sát , điều này chỉ ra rằng nam và nữ giới không cùng y kiến về tác hại của khói thuốc lá .
c.
* Xác suất của câu trả lời từ người nữ nói “có” trong số người nói “có” , là : P(nữ|có) = n(nữÇcó) / n(có) = 256 / 418 » 0.61 = 61% . Nghĩa là xấp xỉ 61% là nữ nói “có” trong số người nói “có” .
* Xác suất của câu trả lời từ người nam nói “có” trong số người nói “có” , là : P(nam|có) = n(namÇcó) / n(có) = 162 / 418 » 0.39 = 39% . Nghĩa là xấp xỉ 39% là nam nói “có” trong số người nói “có” .
d.
* Xác suất của câu trả lời từ người nam nói “có” trong toàn thể là P(có|nam) = n(cóÇnam) / n(S) = 162/600 » 0.27 = 27% ( không điều kiện non-conditional)
* Xác suất của câu trả lời từ người nữ nói “có” trong toàn thể P(có|nữ) = n(cóÇnữ) / n(S) = 256/600 » 0.42 = 42% (không điều kiện non-conditional)
Luật nhân xác suất - The Product Rule
Với mọi biến cố A và B bất kỳ , xác suất của biến cố A và B là
Sơ đồ cây - Tree Diagram
Ta thường dùng sơ đồ cây để giải các bài toán cụ thể , có thể hình dung như sau
Ví dụ . Hai lá bài được rút ra từ bộ bài 52 lá . Tính xác suất để có 2 con cơ .
Lời giải .
Ta xét sơ đồ cây sau
Ở nhánh thứ nhất , xác suất để có Lá 1- Cơ
là P(Lá 1- Cơ) = 13/52 .
Nhánh thứ hai , xác suất để có Lá 2- Cơ là
P(Lá 2- Cơ| Lá 1-Cơ) = 12/51 .
Xác suất cần tìm là P(Lá 1 - Cơ và Lá 2 –Cơ ) :
Theo công thức nhân xác suất ,
P(Lá 1 -Cơ và Lá 2 -Cơ) =
P(Lá 2 -Cơ | Lá 1 -Cơ) x P( Lá 1-Cơ) = 12/51 x 13/52 .
Ví dụ . Có 2 túi I và II . Túi I có 3 bi đỏ , 2 bi vàng . Túi II có 1 bi đỏ , 4 bi vàng . Chọn một bi trong một túi bằng cách tung đồng xu . Tính xác suất để có một bi vàng .
Lời giải .
Ta phân tích sơ đồ cây sau
Ở túi I , xác suất để có 1 bi vàng
là P1(vàng) = ½ . 2/5
Ở túi II , xác suất để có 1 bi vàng
là P2(vàng) = ½ . 4/5
Xác suất để có bi vàng là P(vàng) = P1(vàng) + P2(vàng) = 3/5
*************************************************
Trần hồng Cơ
10/10/2012
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
-------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
Pure mathematics is, in its way, the poetry of logical ideas.
Albert Einstein .
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
TOÁN THỰC HÀNH CHƯƠNG 2 . 2.2
Bài giảng .
2. 2 THỐNG KÊ - STATISTICS , HỒI QUY TUYẾN TÍNH - LINEAR REGRESSION .
Chủ đề
- Tổng thể (Population) , Mẫu (sample) , Dữ liệu (data) .
- Phân phối chuẩn (normal distribution) .
- Hồi quy tuyến tính (Linear regression) .
Ứng dụng
- Tung súc sắc .
- Nghiên cứu diễn đàn .
- Giá xăng dầu .
- Tuổi lao động .
- Khảo sát chiều cao .
- Tỷ lệ thất nghiệp .
Khái niệm cơ bản
* Khái niệm ( Tổng thể – Mẫu –Dữ liệu ) .
* Độ đo trung tâm -Measure of centrality ( Trung bình (Mean) –Trung vị (Median) –Mốt (Mode ) )
* Độ đo phân tán -Measure of dispersion ( Phương sai (Variance) –Độ lệch (Deviation) –Độ lệch chuẩn (Standard deviation) )
* Phân phối chuẩn (The normal distribution) - Biến rời rạc và biến liên tục -Discrete and continous variables.
* Hồi quy tuyến tính (Linear Regression) ( Điều hóa tốt nhất (Best fit) –Hệ số tương quan tuyến tính (Coefficient of linear correlation ) )
1. TỔNG THỂ - MẪU – DỮ LIỆU .
· Tập hợp các phần tử được khảo sát gọi là tổng thể . Tập con bất kỳ của tổng thể gọi là mẫu . Khi khảo sát một tổng thể quá lớn ta không thể thu thập được tất cả các dữ liệu của mọi phần tử vì thế ta phải thu thập các dữ liệu của một mẫu nhỏ và dễ quản lí hơn .
· Mẫu được xem là mẫu tốt “good sample” khi nó có thể đại diện cho tổng thể .
· Khi đã thu thập đầy đủ dữ liệu ta có thể tổng kết bằng cách tính toán những thống kê mô tả khác nhau . Dữ liệu mẫu được thu thập và tóm tắt sẽ giúp chúng ta đưa ra kết luận hợp lý về tổng thể .
Lập bảng phân phối tần số - Constructing A Frequency Distribution
* Nếu dữ liệu thô có ít giá trị khác nhau ta liệt kê các điểm dữ liệu riêng biệt . Ngược lại , nếu dữ liệu thô gồm nhiều giá trị khác nhau ta tạo các khoảng và làm việc theo dữ liệu nhóm .
* Kiểm đếm số lượng các điểm dữ liệu trong mỗi khoảng thời gian hoặc số lần xuất hiện các dữ liệu cá thể .
* Liệt kê tần số của mỗi khoảng thời gian hoặc mỗi điểm dữ liệu cá thể .
* Tìm tần số tương đối bằng cách chia tần số của của mỗi khoảng thời gian hoặc số lần xuất hiện các dữ liệu cá thể với tổng số các điểm dữ liệu có trong phân phối ( kết quả được ghi là % ) .
1.1 Dữ liệu riêng biệt - Distinct Data
Ví dụ . Tung con súc sắc đồng chất , ta có kết quả các mặt như sau
1 1 2 5 5 6 1 6 5 3
6 1 1 3 3 6 5 6 6 1
4 1 1 3 1 5 6 6 1 6
2 5 4 5 2 3 2 5 1 5
4 2 6 2 1 3 5 4 3 4
Hãy lập bảng phân phối tần số .
Lời giải .
Dùng ESBStats , tạo workbook TUNG SUC SAC , nhập các dữ liệu điểm phân biệt
Click vào Bar Graph xem biểu đồ cột .
Click vào Line Graph xem biểu đồ đường thẳng .
Click vào Descriptive Stats và Main Summary xem các số liệu thống kê mô tả như
Độ tập trung - Measures of Centrality
Trung bình -Mean: 3,5000
Trung vị -Median: 3,5000
Mốt -Mode: 1,0000
Độ phân tán - Measures of Dispersion
Độ lệch trung bình -Mean Deviation: 1,7000
Phương sai -Variance: 3,6020
Độ lệch chuẩn -Standard Deviation: 1,8979
*************************************************
Xem youtube
Click vào link sau download TUNG SUC SAC
1.2 Dữ liệu nhóm - Grouped Data
Ví dụ . Diễn đàn được mở cửa cho người tham dự có tuổi ít nhất là 16 . Điều tra một mẫu gốm có 42 người với số tuổi như sau
26 16 21 34 18 41 38
48 27 22 30 39 62 25
25 38 29 31 28 20 56
60 24 61 28 32 33 18
23 27 46 30 34 62 49
59 19 20 23 24 45 22
Lập bảng phân phối tần số .
Lời giải .
Dùng ESBStats , tạo workbook TUOI DIEN DAN , nhập các dữ liệu nhóm
Click vào Standard Histogram xem biểu đồ cột .
Click vào Pie Graph xem biểu đồ quạt .
Click vào Descriptive Stats và Main Summary xem các số liệu thống kê mô tả như
Độ tập trung - Measures of Centrality
Trung bình -Mean: 34,0952
Trung vị -Median: 30,1538
Mốt -Mode: 26,0000
Độ phân tán - Measures of Dispersion
Độ lệch trung bình -Mean Deviation: 11,1565
Phương sai -Variance: 186,7224
Độ lệch chuẩn -Standard Deviation: 13,6646
Xem hình
*************************************************
Xem youtube
Click vào link sau download TUOI DIEN DAN
1.3 Trung bình (MEAN) , Trung vị (MEDIAN) , Mốt (MODE) ( Độ đo trung tâm -Measures of central tendency )
Trung bình (Mean)
Ví dụ . Giá xăng dầu tại các trạm nhiên liệu khác nhau được khảo sát ( $/gallon ) và có số liệu theo bảng sau . Tìm giá xăng dầu trung bình .
1.399 1.349 1.299 1.429 1.399 1.379 1.259
Ví dụ . Năm 2001 văn phòng thống kê lao động Hoa Kỳ khảo sát tuổi công nhân . Bảng phân phối tần số như sau .
y = tuổi
|
Số công nhân
(f)
| |
16 <= y < 20
|
640,000
| |
20 <= y < 25
|
660,000
| |
25 <= y < 35
|
372,000
| |
35 <= y < 45
|
276,000
| |
45 <= y < 55
|
171,000
| |
55 <= y < 65
|
111,000
| |
n = 2,300,000
| ||
Tìm độ tuổi trung bình của công nhân .
Cách tính trung bình của dữ liệu khoảng
Trung vị -Median Trung vị là giá trị chính giữa trong bảng phân phối các số liệu . Đánh số và xếp thứ tự cho các điểm dữ liệu ,
+ Nếu số điểm dữ liệu là lẻ thì trung vị là giá trị của điểm dữ liệu nằm chính giữa .
+ Nếu số điểm dữ liệu là chẵn thì trung vị là giá trị trung bình của 2 điểm dữ liệu nằm chính giữa .
Lưu ý : Trung vị chia bảng phân phối thành 2 phần có số dữ liệu điểm bằng nhau .
Ví dụ . Tìm trung vị của các bảng phân phối sau .
a. 2 8 3 12 6 2 11
b. 2 8 3 12 6 2 11 8
Lời giải
a. Xếp thứ tự cho các điểm dữ liệu
2 2 3 6 8 11 12 . Vì có 7 điểm dữ liệu ( n = 7 , lẻ ) nên trung vị là 6 .
b. Xếp thứ tự cho các điểm dữ liệu
2 2 3 6 8 8 11 12 . Vì có 8 điểm dữ liệu ( n = 8 , chẵn ) nên trung vị là trung bình của 6 và 8 . Vậy trung vị là ( 6 +8 )/ 2 = 7 .
Dùng công cụ Meta Calculator trên Blog này tìm trung vị . Ở phần Statistic Calculator , nhập dữ liệu điểm
Click vào Basic Stats , đọc các mô tả thống kê
Ta có trung vị (Median ) là 6 . Tương tự cho ví dụ b.
Click vào Basic Stats , đọc các mô tả thống kê
Ta có trung vị (Median ) là 7 .
Dùng công cụ Meta Calculator trên Blog này tìm trung vị . Ở phần Statistic Calculator , nhập dữ liệu điểm
Click vào Basic Stats , đọc các mô tả thống kê
Ta có trung vị (Median ) là 6 . Tương tự cho ví dụ b.
Click vào Basic Stats , đọc các mô tả thống kê
Ta có trung vị (Median ) là 7 .
Mốt -Mode Mốt là dữ liệu xuất hiện nhiều lần nhất trong mẫu , có nghĩa là điểm dữ liệu có tần số cao nhất .
Một bảng phân phối dữ liệu có thể có một hay nhiều mốt hoặc không có mốt .
Ví dụ . Tìm mốt trong bộ dữ liệu sau .
a. 4 10 1 8 5 10 5 10
b. 4 9 1 10 1 10 4 9
c. 9 6 1 8 3 10 3 9
Lời giải .
a. Mốt là 10 , vì tần số xuất hiện nhiều nhất là 3 lần .
b. Không có mốt , vì tần số xuất hiện của các dữ liệu đều bằng nhau .
c. Mốt là 3 và 9 . Phân phối này được gọi là nhị mốt .
1.2 Độ lệch (DEVIATION) , phương sai (VARIANCE) , Độ lệch chuẩn (STANDARD DEVIATION)
( Độ đo phân tán -Measures of dispersion )
Một dữ liệu điểm sát với giá trị trung bình sẽ có độ lệch nhỏ và ngược lại .
Ví dụ . Điểm số của một trò chơi được ghi lại như sau
135 , 155 , 185 , 185 , 200 , 250 .
Tìm giá trị trung bình , độ lệch của mỗi dữ liệu ( độ lệch thành phần ) và trung bình độ lệch .
Lời giải
Ví dụ . Chỉ số tham khảo của mặt hàng máy tính bảng như sau .
135 , 155 , 185 , 185 , 200 , 250 .
Tìm độ lệch chuẩn .
Lời giải .
Nhập dữ liệu vào Statistic Calculator tại Máy tính, vẽ đồ thị, ma trận, thống kê trên Blog này
Click vào Basic Stats , đọc thống kê mô tả .
2. PHÂN PHỐI THƯỜNG -THE NORMAL DISTRIBUTION
Phân phối có biểu đồ gần đối xứng , dạng chuông , với đa số điểm dữ liệu ở trung tâm , được gọi là phân phối thường .
Ví dụ . xem biểu đồ phân phối sau , lưu ý đến 3 chỉ số độ đo trung tâm rất gần nhau .
Độ đo trung tâm -Measures of Centrality
Trung bình -Mean: 16.0020
Trung vị -Median: 16.0034
Mode: 16.0100
2.1 Biến rời rạc – biến liên tục Discrete versus Continous Variables
- Biến gọi là rời rạc nếu có khoảng trống giữa những đữ liệu điểm khác nhau . Ví dụ tuổi của trẻ em trong gia đình .
- Biến gọi là liên tục nếu thể giả sử bất kỳ giá trị nào cũng đều có thể thuộc một khoảng dữ liệu được sắp xếp . Ví dụ chiều cao của học sinh .
Phân phối thường có 2 tính chất chính .
1. Tần số của các điểm dữ liệu gần trung tâm ( hoặc trung bình ) là cao hơn tần số của các điểm dữ liệu xa trung tâm .
2. Phân phối có tính đối xứng .
Vì những tính chất này nên trung bình , trung vị và mốt hầu như gần ở trung tâm phân phối .
Ví dụ . Chiều cao của nhóm người được điều tra giả sử có thể mô tả bởi phân phối thường . Trung bình chiều cao là 66.5 inches , độ lệch chuẩn là 2.4 inches . Tìm và giải thích các khoảng biểu diễn cách đều 1 , 2 và 3 độ lệch chuẩn từ giá trị trung bình . ( xem hình )
2.2 Xác suất và diện tích -
Tìm xác suất một biến ngẫu nhiên x trong khoảng từ a đến b , ta phải xác định diện tích của hình phẳng giới hạn từ a đến b .
2.3 Phân phối chuẩn -The Standard Normal Distribution
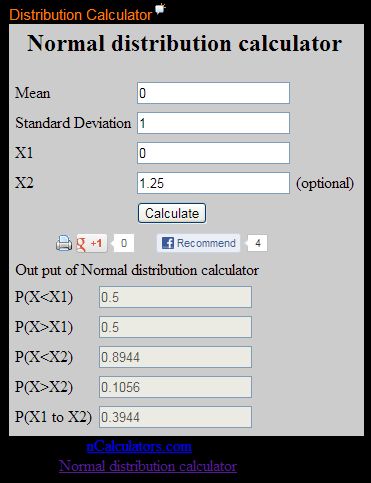
Phân phối chuẩn là phân phối thường có trung bình bằng 0 và độ lệch chuẩn bằng 1 . Ta còn gọi phân phối chuẩn là phân phối Z .
Bạn có thể sử dụng phần mềm Distribution Calculator trực tuyến dưới đây , nhập giá trị trung bình , độ lệch chuẩn , X1 , X2 và click Calculate . Đọc kết quả ở phần P(X1 to X2)
**********************************************************************
b. p( z > 1.87 ) Dùng ESBPDF Analysis
Dùng phần mềm Distribution Calculator trực tuyến .
Đọc kết quả ở phần P(X > X1)
Tương tự cho các ví dụ c. và d.
2.4 Đổi sang phân phối Z - Converting to the Z-Distribution .
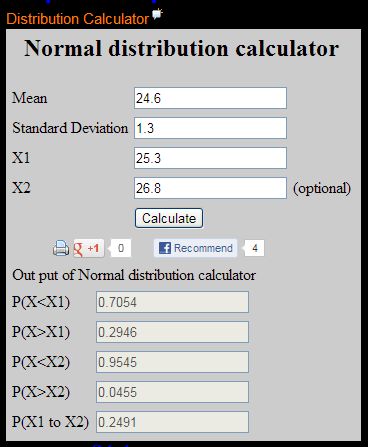
Ví dụ . Giả sử rằng tổng thể được bởi phân phối thường có mu = 24.6 và độ lêch chuẩn sigma = 1.3 . Hỏi có bao nhiêu phần trăm dữ liệu trong khoảng 25.3 và 26.8 ?
Dùng phần mềm Distribution Calculator trực tuyến .
Đọc kết quả ở phần P(X1 to X2)
Dùng phần mềm Distribution Calculator trực tuyến .
Đọc kết quả ở phần P(X1 to X2)
Như vậy có xấp xỉ khoảng 24.9% dữ liệu trong khoảng 25.3 và 26.8 .
Ví dụ . Chiều cao của nhóm người Nhật được xem như có dạng phân phối thường . Trung bình chiều cao là 68 inches , độ lệch chuẩn là 4 inches . Tìm xác suất của các biến cố sau
a. cao hơn 73 inches
b.trong khoảng 60 và 75 inches .
2.5 Biên sai - Margin of Error ( MOE )
Ví dụ . Giả sử rằng với độ tin cậy 90% trong chiến dịch bầu cử , hãy tìm biên sai trong các trường hợp sau
a. kích thước mẫu n = 275
b. kích thước mẫu n = 750
Nhập liệu như hình sau , đọc MOE ( Margin of Error )
Điều này nghĩa là từ cuộc điều tra mẫu có 275 người , ta có độ tin cậy khoảng 90% mà sai số khả dĩ lớn nhất trong quy mô mẫu có thể cộng thêm hay bớt đi 5% điểm dữ liệu .
truy cập vào link sau http://www.relevantinsights.com/research-tools
Nhập liệu như hình sau , đọc MOE ( Margin of Error )
Ví dụ . Trong cuộc điều tra 500 sinh viên đang học tại Đại học Yale , có 410 người trả lời rằng họ sẽ tốt nghiệp sau 4 năm .
a. Tìm quy mô mẫu thỏa mãn điều kiện tốt nghiệp sau 4 năm .
b. Với độ tin cậy 95% , tìm biên sai MOE .
c. Giải thích các số liệu thu được .
Lời giải .
a. Quy mô mẫu là 410/500 = 0.82 = 82%
b.
c. Như vậy với độ tin cậy 95% thì biên sai là 4.4% , khi đó quy mô mẫu sẽ là 82% + (-) 4.4% . Đây là tỷ lệ sinh viên cho rằng sẽ tốt nghiệp sau 4 năm học .
Nói cách khác là có khoảng từ 77.6% đến 86.4% tỷ lệ sinh viên Đại học Yale cho rằng sẽ tốt nghiệp sau 4 năm học .
3 . HỒI QUY TUYẾN TÍNH -LINEAR REGRESSION .
3.1 Công thức hồi quy tuyến tính .
3.1 Công thức hồi quy tuyến tính .
Xét hai điểm cho trước (x1,y1) và (x2,y2) , giả thiết rằng x , y có quan hệ tuyến tính , khi đó ta sẽ tìm được đường thẳng nối 2 điểm này . Quá trình tìm phương trình đường thẳng này gọi là hồi quy tuyến tính . Phương trình thỏa mãn tính chất này được gọi là mô hình toán học của quan hệ tuyến tính .
Khi các dữ liệu điểm chi ra khuynh hướng tuyến tính , ta có thể thiết lập đường thẳng xấp xỉ tốt nhất . Đường thẳng này được gọi là đường điều hóa tốt nhất ( BFL , Best-fitted Line ) .
Ví dụ : Cho các điểm (5,14),(9,17),(12,16),(14,18),(17,23)
a. Tìm đường điều hóa tốt nhất (BFL)
b. Chấm tọa độ các điểm và vẽ đồ thị của BFL trên cùng mạt phẳng tọa độ .
a. Tìm đường điều hóa tốt nhất (BFL)
b. Chấm tọa độ các điểm và vẽ đồ thị của BFL trên cùng mạt phẳng tọa độ .
Lời giải .
Xét bảng số liệu sau .
Dùng công thức tính b và a .
LƯU Ý KỸ THUẬT
Sau khi mô hình của tập hợp dữ liệu đã được tìm thấy, nó có thể được làm tròn cho mục đích báo cáo. Tuy nhiên, không sử dụng một mô hình làm tròn trong khi tính toán, và cũng không làm tròn đáp số trong quá trình tính toán, trừ khi có quy định khác. Khi mô hình được sử dụng để tìm các đáp số ngoại suy hay nội suy khác , nên được làm tròn một cách thích hợp với yêu cầu bài toán , và khi kiểm tra lại không có độ chính xác quá sai biệt so với các xuất liệu gốc .
Ví dụ * Phát tán khí thải Luợng khí thải phát tán ở Hoa Kỳ từ 1986 đến 1995 được cho ở bảng dưới đây
Năm
|
Khí thải ( tấn )
|
Năm
|
Khí thải ( tấn )
|
1986
|
109,199
|
1991
|
93,376
|
1987
|
108,012
|
1992
|
94,043
|
1988
|
115,849
|
1993
|
94,133
|
1989
|
103,144
|
1994
|
98,779
|
1990
|
100,650
|
1995
|
92,099
|
- Sắp xếp các đữ liệu với x là số năm sau 1980 và y là khối lượng khí thải phát tán ( tấn ) . Vẽ các điểm dữ liệu này .
- Viết phương trình đường điều hóa tốt nhất cho các điểm dữ liệu (BFL) .
- Vẽ đồ thị của mô hình tuyến tính trên cùng hệ trục tọa độ với các điểm dữ liệu .
- So sánh sự thay đổi của sự phát tán hằng năm và độ dốc của đường điều hóa tốt nhất BFL .
Lời giải
a. Từ 1986 đến 1995 , ta sắp xếp lại dữ liệu của x , chọn x = 0 biểu diễn cho 1980 ,
Năm
|
Khí thải ( tấn )
|
Năm
|
Khí thải (tấn)
|
6
|
109,199
|
11
|
93,376
|
7
|
108,012
|
12
|
94,043
|
8
|
115,849
|
13
|
94,133
|
9
|
103,144
|
14
|
98,779
|
10
|
100,650
|
15
|
92,099
|
Dùng CurveExpert tìm BFL .
Nhập và vẽ các điểm dữ liệu .
b. Click vào Apply Fit - > chọn Linear Fit
 |
| Thêm chú thích |
Click Info xem kết quả tìm b và a .
3.2 Hệ số tương quan tuyến tính .
Ta luôn luôn có thể tìm được BFL cho bất kỳ các tập điểm dữ liệu , nhưng độ chính xác là bao nhiêu để đường thẳng tìm được có thể đáp ứng cho mô hình toán học đó ?
Nếu những điểm dữ liệu phân tán xa BFL thì đây là quan hệ tuyến tính yếu . Ngược lại nếu chúng tập trung gần với BFL ta có mối quan hệ tuyến tính mạnh và BFL có thể đại diện cho những dự báo nội suy hoặc ngoại suy tốt .
Độ mạnh của khuynh hướng tuyến tính có thể được mô tả bởi hệ số tương quan tuyến tính , ký hiệu là r .
Một cách tổng quát , r càng gần -1 và 1 , khuynh hướng tuyến tính giữa x và y càng mạnh khi đó BFL có thể áp dụng cho dự báo một cách đáng tin cậy . Nếu r gần 0 , quan hệ tuyến tinh giữa x và y yếu đi , BFL không cho ta những kết quả dự báo tốt .
Ví dụ . Cho các diểm dữ liệu sau
(5,14),(9,17),(12,16),(14,18),(17,23) .
(5,14),(9,17),(12,16),(14,18),(17,23) .
Tìm hệ số tương quan tuyến tính r ?
Lời giải .
Ví dụ . * Thất nghiệp và thu nhập cá nhân . Bảng dữ liệu sau chỉ ra tỷ lệ thất nghiệp và tổng thu nhập cá nhân tại Hoa Kỳ theo các năm tương ứng .
- Dùng hồi quy tuyến tính để dự báo tổng thu nhập cá nhân nếu tỷ lệ thất nghiệp là 5% ( nội suy ).
- Dùng hồi quy tuyến tính để dự báo tỷ lệ thất nghiệp nếu tổng thu nhập cá nhân là $10 billion ( 10 tỷ USD ) ( ngoại suy ) .
- Những dự báo ở câu (a) và (b) có đáng tin cậy không ? Giải thich ?
Năm
|
Tỷ lệ thất nghiệp
( % )
|
Tổng thu nhập cá nhân
(Tỷ $USD )
|
1975
|
8.5
|
1.3
|
1980
|
7.1
|
2.3
|
1985
|
7.2
|
3.4
|
1990
|
5.6
|
4.8
|
1995
|
5.6
|
6.1
|
2000
|
4.0
|
8.3
|
Lời giải
- Nhập và vẽ các điểm dữ liệu bằng Curve Expert với x là tỷ lệ thất nghiệp , y là tổng thu nhập .
Linear fit để tìm các hệ số của BFL .
c. Với hệ số tương quan tuyến tính r = -0.970438 sát với -1 , có thể kết luận những dự báo này là có độ tin cậy tốt , quan hệ tuyến tính giữa x và y có mức độ mạnh .
Ngoài ra , vì r <0 , ta có thể nói rằng tổng thu nhập cá nhân y ( total personal income ) giảm dần khi tỷ lệ thất nghiệp x ( unemployment rate ) gia tăng .
**************************************************************
Trần hồng Cơ
30/10/2012
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
TOÁN THỰC HÀNH CHƯƠNG 2 . 2.3
Bài giảng .
2. 3 TÀI
CHÍNH CƠ BẢN .
Chủ đề
- Tiền lãi .
- Lợi tức đồng niên-Tiền góp hằng năm (Annual yield –annuity) .
- Khoản vay (Loans) .
Ứng dụng
- Vay mượn (Borrowing) .
- Khoản góp hằng tháng (Monthly payment) .
- Kết số (Future value) .
- Thực số (Present value) .
Khái niệm cơ bản
* Tiền lãi ( Lãi đơn
-Simple –Lãi kép- Compound – Lãi trả góp -Add -on interest
) .
* Lợi tức đồng niên – Tiền góp hằng năm – Quỹ chìm (Annual yield
-Annuity –Sinking fund ).
* Khoản vay -Loans
( Vay trả góp -Amortized Loan –Lịch trả góp-Amortized schedule - APR )
1. TIỀN LÃI - INTEREST
Số tiền ban đầu cho vay được
gọi là vốn hoặc thực số . Nếu một số vốn đã được trả lại, sau đó là phần còn lại
chưa thanh toán được gọi là dư nợ gốc, hoặc tài khoản có . Tổng số tiền cho vay
được trả lại được gọi là kết số , bao gồm số tiền ban đầu cho vay và lợi nhuận
hoặc tiền lãi của người cho vay . Tiền lãi sẽ được thanh toán phụ thuộc vào tỷ lệ
lãi suất.
1.1 Lãi đơn - Simple
interest
Lãi đơn I tính
trên vốn P theo lãi suất định kỳ năm r với số năm t là
I = P r
t
Kết số FV của
vốn P
lãi suất định kỳ năm r với số năm t là
FV = P (
1 +
r t )
Ví dụ . Cửa hàng tạp hóa ABC đã vay $340,000
lãi suất định kì năm 5.1% trong
120 ngày để mua hàng mùa Giáng sinh . Tìm
tiền lãi phải trả ?
Lời giải .
Ta có vốn P =
340,000 lãi suất r =
5.1% = 0.051
1
năm --- 365 ngày
t?
năm --- 120 ngày
Thời
gian
t
= 120 ngày =
120/365 ( năm)
I = P r
t = 340,000 x 0.051 x 120/365 =
5700.8219 » $5700.82
Ví dụ . Để trả tiền nhập hàng , Cửa hàng tạp hóa ABC đã vay $185,000 lãi suất
năm 7.3% trong 4 tháng . Tìm kết số FV của khoản vay .
Lời giải .
Ta có vốn P = $185,000 ,
lãi suất năm r = 7.3%
= 0.073
1
năm --- 12 tháng
t?
năm --- 4 tháng
Thời gian 4 tháng = 4/12 năm
Áp dụng FV = P ( 1
+ r t )= 185,000 x 0.073 x 4/12 = 189501.6667
» $189501.67 .
Điều này nghĩa là cửa hàng
ABC phải trả $185,000 cộng thêm $4501.67 tiền lãi vào cuối
kỳ vay 4 tháng .
Ví dụ . Tìm số vốn cần đầu
tư hiện nay ( present value -thực số ) với lãi suất 0.0575 để thu
được $1000 trong 2 năm .
Lời giải .
FV = P ( 1
+ r t ) hay
P = FV/ ( 1 + r t )
P = FV/ ( 1 + r t )
Ta có
FV = 1000
; r =
0.0575 ; t
= 2
hay P = 1000 / ( 1
+ 0.0575 . 2 ) = 896.86
Vậy vốn đầu tư hiện nay ( thực số )
là $896.86
1.2 Lãi trả góp - Add-on
interest
Lãi đơn có kết số được chia đều thành mỗi kỳ
trả bằng nhau ta gọi là lãi trả góp , kí hiệu
AoI
Ví dụ . Eddie mua một laptop trị giá $1,300
ở Wall-Mart . Anh ấy trả trước $200 và chấp thuận trả góp với lãi suất 10% lãi trả dần trong 2 năm . Tìm số tiền trả góp hằng tháng .
Lời giải .
P = khoản
vay = 1,300 -
200 = 1,100 ($) ;
Lãi suất r = 0.1
; thời gian t =
2 (yrs)
Vậy FV = P (
1 +
r t ) = 1,100 . ( 1 + 0.1 x 2 ) =
1,320 ($)
AoI
= FV / t = 1,320 / 24 = $55/
tháng .
1.3 Công thức lãi kép -Compound Interest Formula
Tại cuối mỗi n kỳ , kết số của vốn ban đầu P
tính theo lãi kép với lãi suất r định kỳ năm và t là thời gian (năm) . Ta có
Trong đó
r lãi suất định kỳ năm ( the annual interest
rate)
i lãi suất định kỳ ( the periodic interest rate ) = r . t
n là số kỳ
.
I tiền
lãi ( the interest) .
Ví dụ . Với
số vốn $1,000 gửi vào tài khoản với 8%
lãi kép định kỳ quí (interest compounded
quartly) . Tìm kết số ( FV ) sau 6 tháng .
+ Tính theo công thức lãi đơn :
Vì lãi kép định kỳ quí , tiền lãi sẽ được tính và tích lũy vào vốn ban đầu mỗi quí .
Cuối quí thứ nhất ta có ,
P = 1,000 ,
r = 0.08 , t = ¼
FV = P (
1 +
r t ) = 1000( 1 + 0.08x1/4 ) =
1020
Cuối quí
thứ nhất ta có ,
P
= 1,020 , r = 0.08 , t = ¼
FV = P (
1 +
r t ) = 1020( 1
+ 0.08x1/4 ) = 1040.40
+ Tính
theo công thức lãi kép :
1 năm --- 4
quí
t? năm --- 1
quí => t = ¼ năm
Lãi suất định kỳ i
= r . t = 0.08 x ¼
= 0.02 ,
1 kỳ ( quí ) ---
3 tháng
n kỳ ? ---
6 tháng => n = 2 kỳ
áp dụng công thức lãi kép
Ví dụ .
a. Tìm kết số FV của khoản
vốn $2,000 gửi vào tài khoản lãi suất
10.3% định kỳ ngày trong 15 năm .
b. Tìm tiền lãi thu được .
Lời giải .
Ví dụ .
a. Tìm kết số FV của khoản
vốn $2,500 gửi vào tài khoản lãi suất
10.3% định kỳ ngày trong 15 năm .
b. Tìm tiền lãi thu được .
Lời giải .
a. Lãi kép định kỳ ngày :
P = 2,500 ,
r = 10.3% = 0.103
,
1 năm --- 365 ngày
t ? năm ---
1 ngày
thời gian t = 1/365
Lãi suất định kỳ i = r . t
= 0.103 x( 1/365 )
365 kỳ (ngày) ---
1 năm
n kỳ ? --- 15 năm => n
= 15 x 365 = 5,475 kỳ
áp dụng công thức lãi kép
b. Vốn là
$2,500 và kết số FV là $11,717.37
, vậy tiền lãi thu được = Kết số (FV)
- Vốn (P) = 11,717.37 - 2,500 = 9,217.37 ($)
Dưới đây là bảng so sánh từng năm giữa lãi
đơn , lãi kép định kỳ năm , quí , tháng và ngày với cùng một khoản vốn $1000 ,
cùng lãi suất 10% và cùng kỳ 10 năm .
2. LỢI TỨC ĐỒNG
NIÊN – TIỀN GÓP HẰNG NĂM ( ANNUAL YIELD
- ANNUITY )
2.1 Lợi tức đồng niên - Annual yield
Lợi tức đồng niên của khoản tiền gửi lãi suất
kép là lãi suất đơn có cùng một kết số với lãi suất kép đó thu được trong 1 năm
. Tìm lợi tức đồng niên bằng cách giải phương trình sau tìm r .
Ví dụ . Tìm lợi tức đồng niên của $2500 gửi vào tài
khoản lãi kép 10.3% định kỳ ngày trong
15 năm .
Lời giải .
Ví dụ . Tìm lợi tức đồng niên tương ứng với lãi suất
ấn định là 8.4% lãi kép định kỳ tháng (compounded
monthly) .
Lời giải .
Tính lãi kép trong 1 năm
Vậy lợi tức đồng niên là 8.73%
2.2 Tiền góp hằng năm - Annuity
Tiền góp hằng năm là dãy những khoản góp đều đặn bằng nhau
vào tài khoản trong đó mỗi khoản đóng nhận một lãi suất kép .
Ví dụ . Đóng $50 hàng tháng với lãi suất 10% .
Tính kết số thu được trong 40
năm với :
a. Lãi đơn .
b. Lãi kép định kỳ tháng .
Lời giải .
a.
Lãi
đơn : $50 x tháng x 40 năm = $24,000
b.
Lãi
kép :
t = 1/12
i =
r. t =
0.1x 1/12 = 0.0083
n
= 40 x 12 = 480 kỳ
* Kết số FV
của tiền góp hằng năm thông thường với khoản góp pymt = $50 , lãi suất định kỳ i = 0.1/12
, và n = 480 lần đóng là :
$ 316,204 * Kết số FV của tiền góp hằng năm đáo hạn với khoản góp pymt = 50$ , lãi suất định kỳ i = 0.1/12 , và n = 480 lần đóng là :
$318,839
2.3 Quỹ chìm -
Sinking Fund là khoản góp hằng năm được
tiết kiệm dùng vào mục đích cá nhân nào đó .
Ví dụ . Jack và Anna muốn lập một quỹ chìm dành cho
việc học tập của đứa con của họ . Biết quỹ này có tài khoản tiền góp hằng năm
thông thường , để có ngân quỹ $30,000 trong 18 năm , lãi suất 9¼ % lãi kép định kỳ 2 tuần , họ phải đóng tiền
góp mỗi kỳ là bao nhiêu ?
Lời giải .
Từ
công thức
tiền góp mỗi kỳ ( 2 tuần ) là $24.9950 ~ $25 .
Ví dụ . Lấy ví
dụ như trên . Hãy tính
a. Kết số thực của quỹ chìm .
b. Số tiền thực đóng của Jack và Anna .
c. Tổng tiền lãi của quỹ chìm .
Lời
giải .
a. Như đã biết pymt =
$25 ,
i = r.t =
0.0925´1/26 ; n = 18
´ 26 = 468
Từ
công thức
Kết số thực của quỹ chìm là $30,000.95
b. Số tiền thực đóng của Jack và Anna là :
468 kỳ x $25/kỳ = $11,700 .
c. Tổng tiền lãi của quỹ chìm = FV - Số tiền thực đóng
= $30,005.95 – $11,700 = $18,305.95
2.4
Tiền góp hằng năm hoãn thuế -
Tax-Deferred Annuity ( TDA )
Là khoản tiền góp hằng
năm dành cho hưu trí .
Ví dụ . Paul .K
vừa tìm được công việc mới , anh
ta muốn lập một quỹ hưu trí TDA . Paul mở một tài khoản tiền góp hàng năm thông
thường bằng cách đóng $200 / tháng , lãi suất 8¾ % , lãi kép định kỳ tháng .
a.
Tìm kết số FV của
quỹ TDA trong 35 năm sau .
b.
Tìm tiền lãi
của quỹ TDA này .
kết số FV của quỹ TDA trong 35 năm sau là $552539.95 ~ $552,540
b .Tiền lãi của quỹ TDA này = Kết số FV - số tiền thực đóng =
$552,540 - $200 x 420 = $468,540
3. KHOẢN VAY - LOANS
3.1 Vay trả
góp - Amortized Loan là khoản
vay mà vốn vay và lãi được trả thành nhiều đợt định kỳ với một khoản bằng nhau
.
Trong đó pymt
là khoản trả góp , i là lãi suất định kỳ (periodic interest rate ) ,
n là số kỳ (number of periods ) ,
P là thực số ( Present Value - PV) hay
là tổng món nợ .
Công thức này dùng để xác định 1 trong số 4 tham
số { pymt
, i, n , P } nếu có 3 tham số kia
.
Ví dụ . George mua
chiếc xe hơi trị giá $13,518.77 . Anh ta
trả trước $1,000 và vay trả góp lãi đơn 4-năm
từ US Bank với lãi suất 12% định kỳ tháng . Tìm các khoản sau
a. Khoản góp phải trả hằng tháng .
b. Tổng tiền lãi của khoản vay .
Lời
giải .
a. Các tham số cho trước :
P = khoản vốn vay = 13,518.77 - 1,000 =
12,518.77 $
r =
12% =
0.12 ; i = r.t =
0.12 x 1/12
n
= 4 x 12 ( kỳ )
Tìm pymt ?
Từ công thức

Khoản góp phải trả hằng tháng là $329.67 ( gồm vốn vay và lãi - principal and interest )
b. George
trả 48 kỳ với $ 329.67 / kỳ
Nên tổng số tiền phải trả
là :
48 x 329.67 $ = $15824.16
Tổng
tiền lãi của khoản vay = tổng số tiền phải trả – vốn vay
= $15824.16
- $12,518.77
= $3,305.39
3.2 Lịch trả
góp - Amortization Schedule . Mỗi khoản trả góp bao gồm vốn vay và lãi . Lịch trả
góp là một bảng kê các kỳ trả góp trong đó chỉ ra tiền vốn vay , phần lãi và số tiền còn lại phải trả sau mỗi kỳ hoàn tất trả góp ( số dư nợ ).
Ví dụ . Với ví dụ như trên ta thiết lập lịch trả góp
cho khoản vốn vay trả góp lãi đơn 4-năm của George trong 4 tháng đầu tiên .
Lời giải .
Khoản vốn vay là $12,518.77 , trả góp trong 48 tháng . Tiền
góp tháng là $329.67 .
Ta có r =
12% = 0.12 ,
t = 1 tháng = 1/12 (năm) ,
P =12,518.77 .
*Kỳ 1 : Tiền lãi đơn I
= Prt =
12,518.77 x 0.12 x 1/12 = 125.1877 ~ $125.19
Trả vốn kỳ 1 : $329.67
- $125.19 = $204.48
( vốn = tiền góp – lãi )
Số dư nợ còn lại phải trả
$12,518.77 -
$204.48 = $12,314.29
*Kỳ 2 : Tiền lãi đơn I = Prt =
12,314.29 x 0.12 x 1/12 = 123.1429 ~ $123.14
Trả vốn kỳ 2 : $329.67
- $123.14 = $206.53
(vốn = tiền góp – lãi )
Số dư nợ còn lại phải trả
$12,314.29 - $206.53 =
$12,107.76
*Kỳ 3 : Tiền lãi đơn I = Prt =
12,107.76 x 0.12 x 1/12 =
121.0776 ~ $121.08
Trả vốn kỳ 3 : $329.67
- $121.08 = $208.59
(vốn = tiền góp – lãi )
Số dư nợ còn lại phải trả
$12,107.76 -
$208.59 = $11899.17
*Kỳ 4 : Tiền lãi đơn I = Prt =
11899.17 x 0.12 x 1/12 = 118.9917
~ $119
Trả vốn kỳ 4 : $329.67
- 119$ = $210.67
(vốn = tiền góp – lãi )
Số dư nợ còn lại phải trả
$11899.17 -
$210.67 = $11688.5
Dưới đây là một đoạn Maple code , tác giả đã soạn thảo cho việc tính khoản tiền góp và lịch trả góp ( ver 6.0 )
> restart; with(finance);
> eqPRESENTVALUE:=P*(1+i)^n=Pymt*((1+i)^n-1)/i:solve(eqPRESENTVALUE,{Pymt});n:=48;i:=0.12/12;P:=12518.77;; ;PV:=solve(eqPRESENTVALUE,{Pymt});
Hướng dẫn :
Trong phần này vốn vay P = 12518.77 , số kỳ n = 48 ( 4 năm , mỗi năm 12 kỳ ) , lãi suất định kỳ i = r.t = 0.12 /12
ta tìm được pymt = 329.667
Hướng dẫn :
Nhập khoản vốn vay P = 12518.77 khoản
khoản tiền góp 329.667 và i = r.t = 0.12 /12
vào đoạn code sau
> A:= amortization(12518.77,329.667, 0.12/12);
> amortization_table[n, Payment, Interest, Principal, Balance] = matrix(A[1]);
Đoạn code này sẽ tính kỳ và tạo lịch trả góp , phần số liệu trong khung đỏ chỉ ra lịch trả góp của George trong 4 tháng đầu tiên .
Bạn có thể dùng công cụ trực tuyến tại
 http://www.javascriptsource.com/repository/javascripts/2003/03/111241/interest.html
http://www.javascriptsource.com/repository/javascripts/2003/03/111241/interest.htmlNhập số liệu như hình sau và click Compute .
hoặc truy cập :

http://www.javascriptsource.com/repository/javascripts/1999/02/26/JS_17387/script17387.html
Nhập số liệu như hình sau và Click Monthly Payment để biết tiền góp hằng tháng ; Click Amortize This để xem lịch trả góp .
Kết quả như sau

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
-------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
Pure mathematics is, in its way, the poetry of logical ideas.
Albert Einstein .
















































































































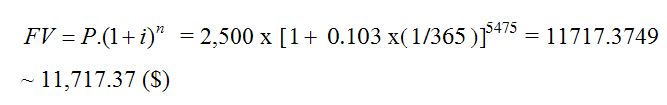






















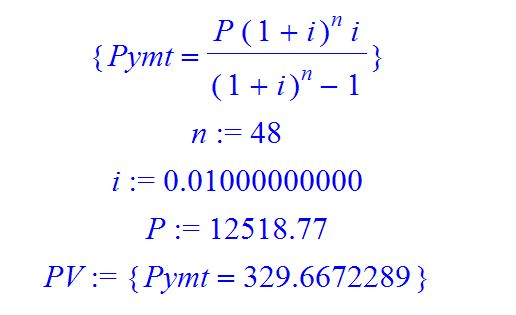







Cohtran-toan-don-gian.blogspot.nl is ranked #12,326 in the world, a low rank means that this website gets lots of visitors. This site is worth $663,750 USD and advertising revenue is $1,818 USD per day. it has 203,700 visitors and 484,806 pageviews per day. Currently, this site needs more than 9.25 GB bandwidth per day, this month will needs more than 277.41 GB bandwidth. Its seo score is 51.2%. IP address is 173.194.35.172, and its server is hosted at Mountain View, United States. Last updated on Thu, 14 Jun 2012 17:29:04 GMT.
Trả lờiXóaAlexa Rank: #12,326
SEO Score: 51.2% (How to optimize cohtran-toan-don-gian.blogspot.nl?)
Daily Visitors: 203,700
Daily Pageviews: 484,806
Daily Bandwidth: 9.25 GB (277.41 GB/month)
Daily Revenue: $1,818 USD
Website Worth: $663,750 USD
Rating:
Xóa3.0/5.0 Stars by StatsCrop