This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
TOÁN THỰC HÀNH CHƯƠNG 2 . 2.2
Bài giảng .
2. 2 THỐNG KÊ - STATISTICS , HỒI QUY TUYẾN TÍNH - LINEAR REGRESSION .
Chủ đề
- Tổng thể (Population) , Mẫu (sample) , Dữ liệu (data) .
- Phân phối chuẩn (normal
distribution) .
- Hồi quy tuyến tính (Linear regression) .
Ứng dụng
- Tung súc sắc .
- Nghiên cứu diễn đàn .
- Giá xăng dầu .
- Tuổi lao động .
- Khảo sát chiều cao .
- Tỷ lệ thất nghiệp .
Khái niệm cơ bản
* Khái niệm ( Tổng thể – Mẫu –Dữ liệu ) .
* Độ đo trung tâm -Measure of centrality ( Trung bình (Mean)
–Trung vị (Median) –Mốt (Mode ) )
* Độ đo phân tán -Measure of dispersion ( Phương sai (Variance)
–Độ lệch (Deviation) –Độ lệch chuẩn (Standard deviation) )
* Phân phối chuẩn (The normal distribution) - Biến rời rạc
và biến liên tục -Discrete and continous variables.
* Hồi quy tuyến tính (Linear Regression) ( Điều hóa tốt
nhất (Best fit) –Hệ số tương quan tuyến tính (Coefficient of linear correlation ) )
1. TỔNG THỂ -
MẪU – DỮ LIỆU .
·
Tập
hợp các phần tử được khảo sát gọi là tổng thể . Tập con bất kỳ của tổng
thể gọi là mẫu . Khi khảo sát một tổng thể quá lớn ta không thể
thu thập được tất cả các dữ liệu của
mọi phần tử vì thế ta phải thu thập các dữ
liệu của một mẫu nhỏ và dễ quản lí hơn .
·
Mẫu
được xem là mẫu tốt “good sample” khi nó
có thể đại diện cho tổng thể .
·
Khi
đã thu thập đầy đủ dữ liệu ta có thể tổng kết bằng cách tính toán những thống
kê mô tả khác nhau . Dữ liệu mẫu được thu thập và tóm tắt sẽ giúp
chúng ta đưa ra kết luận hợp lý về tổng thể .
Lập bảng phân phối tần số - Constructing A
Frequency Distribution
* Nếu dữ liệu thô có ít giá trị khác nhau ta liệt kê các điểm
dữ liệu riêng biệt . Ngược lại , nếu dữ liệu thô gồm nhiều giá trị khác nhau ta
tạo các khoảng và làm việc theo dữ liệu nhóm .
* Kiểm đếm số lượng các điểm dữ liệu trong mỗi khoảng thời
gian hoặc số lần xuất hiện các dữ liệu cá thể .
* Liệt kê tần số của mỗi khoảng thời gian hoặc mỗi điểm dữ liệu
cá thể .
* Tìm tần số tương đối bằng cách chia tần số của của mỗi
khoảng thời gian hoặc số lần xuất hiện các dữ liệu cá thể với tổng số các điểm
dữ liệu có trong phân phối ( kết quả được ghi là % ) .
1.1 Dữ liệu riêng biệt - Distinct Data
Ví dụ . Tung con súc sắc đồng chất , ta có kết quả
các mặt như sau
1 1 2 5 5 6 1 6 5 3
6 1 1 3 3 6 5 6 6 1
4 1 1 3 1 5 6 6 1 6
2 5 4 5 2 3 2 5 1 5
4 2 6 2 1 3 5 4 3 4
Hãy lập bảng phân phối tần số .
Lời giải .
Dùng ESBStats , tạo workbook TUNG SUC SAC , nhập các dữ liệu điểm phân biệt
Click vào Bar Graph xem biểu đồ cột .
Click vào Line Graph xem biểu đồ đường thẳng .
Click vào Descriptive Stats và Main Summary xem các số liệu thống kê mô tả như
Độ tập trung - Measures of Centrality
Trung bình -Mean: 3,5000
Trung vị -Median: 3,5000
Mốt -Mode: 1,0000
Độ phân tán - Measures of Dispersion
Độ lệch trung bình -Mean Deviation: 1,7000
Phương sai -Variance: 3,6020
Độ lệch chuẩn -Standard Deviation: 1,8979
*************************************************
Xem youtube
Click vào link sau download TUNG SUC SAC
1.2 Dữ liệu nhóm - Grouped Data
Ví dụ . Diễn đàn được mở
cửa cho người tham dự có tuổi ít nhất là 16 . Điều tra một mẫu gốm có 42 người
với số tuổi như sau
26 16 21 34 18 41 38
48 27 22 30 39 62 25
25 38 29 31 28 20 56
60 24 61 28 32 33 18
23 27 46 30 34 62 49
59 19 20 23 24 45 22
Lập bảng phân phối tần số .
Lời giải .
Dùng ESBStats , tạo workbook TUOI DIEN DAN , nhập các dữ liệu nhóm
Click vào Standard Histogram xem biểu đồ cột .
Click vào Pie Graph xem biểu đồ quạt .
Click vào Descriptive Stats và Main Summary xem các số liệu thống kê mô tả như
Độ tập trung - Measures of Centrality
Trung bình -Mean: 34,0952
Trung vị -Median: 30,1538
Mốt -Mode: 26,0000
Độ phân tán - Measures of Dispersion
Độ lệch trung bình -Mean Deviation: 11,1565
Phương sai -Variance: 186,7224
Độ lệch chuẩn -Standard Deviation: 13,6646
Xem hình
*************************************************Xem youtube
Click vào link sau download TUOI DIEN DAN
1.3 Trung bình (MEAN) , Trung vị (MEDIAN) , Mốt (MODE) ( Độ đo trung
tâm -Measures of central tendency )
Trung
bình (Mean)
Ví dụ . Giá xăng dầu tại các trạm nhiên liệu khác
nhau được khảo sát ( $/gallon ) và có số
liệu theo bảng sau . Tìm giá xăng dầu
trung bình .
1.399 1.349 1.299 1.429 1.399 1.379 1.259
Ví
dụ . Năm 2001 văn phòng thống kê lao động Hoa Kỳ khảo sát tuổi công nhân . Bảng
phân phối tần số như sau .
y
= tuổi
|
Số công nhân
(f)
|
|
16 <= y <
20
|
640,000
|
|
20 <= y <
25
|
660,000
|
|
25 <= y <
35
|
372,000
|
|
35 <= y <
45
|
276,000
|
|
45 <= y <
55
|
171,000
|
|
55 <= y <
65
|
111,000
|
|
n = 2,300,000
|
||
Tìm độ tuổi trung bình của
công nhân .
Cách tính trung bình của dữ liệu khoảng
Trung vị -Median Trung vị là giá trị chính giữa
trong bảng phân phối các số liệu . Đánh số và xếp thứ tự cho các điểm dữ liệu ,
+ Nếu số điểm dữ liệu là lẻ thì trung vị là
giá trị của điểm dữ liệu nằm chính giữa .
+ Nếu số điểm dữ liệu là chẵn thì trung vị
là giá trị trung bình của 2 điểm dữ liệu nằm chính giữa .
Lưu ý : Trung
vị chia bảng phân phối thành 2 phần có số dữ liệu điểm bằng nhau .
Ví dụ . Tìm trung vị của các
bảng phân phối sau .
a. 2
8 3 12
6 2 11
b. 2
8 3 12
6 2 11
8
Lời giải
a. Xếp thứ tự cho các điểm dữ liệu
2 2
3 6 8
11 12 . Vì có 7 điểm dữ liệu ( n = 7 , lẻ ) nên trung vị là 6 .
b.
Xếp thứ tự cho các điểm dữ liệu
2 2
3 6 8
8 11 12
.
Vì có 8 điểm dữ liệu ( n = 8 , chẵn ) nên trung vị là trung bình của 6 và 8 .
Vậy trung vị là ( 6 +8 )/ 2
= 7 .
Dùng công cụ Meta Calculator trên Blog này tìm trung vị . Ở phần Statistic Calculator , nhập dữ liệu điểm
Click vào Basic Stats , đọc các mô tả thống kê
Ta có trung vị (Median ) là 6 . Tương tự cho ví dụ b.
Click vào Basic Stats , đọc các mô tả thống kê
Ta có trung vị (Median ) là 7 .
Dùng công cụ Meta Calculator trên Blog này tìm trung vị . Ở phần Statistic Calculator , nhập dữ liệu điểm
Click vào Basic Stats , đọc các mô tả thống kê
Ta có trung vị (Median ) là 6 . Tương tự cho ví dụ b.
Click vào Basic Stats , đọc các mô tả thống kê
Ta có trung vị (Median ) là 7 .
Mốt -Mode Mốt
là dữ liệu xuất hiện nhiều lần nhất
trong mẫu , có nghĩa là điểm dữ liệu có tần số cao nhất .
Một bảng phân phối dữ liệu có
thể có một hay nhiều mốt hoặc không có mốt .
Ví dụ . Tìm mốt trong bộ dữ liệu sau .
a. 4 10 1
8 5 10
5 10
b. 4
9 1 10
1 10 4 9
c. 9
6 1 8
3 10 3 9
Lời giải .
a. Mốt là 10 , vì tần số xuất hiện nhiều nhất là 3 lần .
b. Không có mốt , vì tần số xuất hiện của các dữ liệu đều bằng
nhau .
c. Mốt là 3 và 9 . Phân phối này được gọi là nhị mốt .
1.2 Độ lệch (DEVIATION)
, phương sai (VARIANCE) , Độ lệch chuẩn (STANDARD DEVIATION)
( Độ đo phân tán
-Measures of dispersion )
Một dữ liệu điểm sát với giá
trị trung bình sẽ có độ lệch nhỏ và ngược lại .
Ví dụ . Điểm số của một trò chơi được ghi lại như sau
135 ,
155 , 185
, 185 , 200
, 250
.
Tìm giá trị trung bình , độ lệch của mỗi dữ
liệu ( độ lệch thành phần ) và trung bình độ lệch .
Lời giải
Ví dụ . Chỉ số tham khảo của mặt hàng máy tính bảng như sau .
135 ,
155 , 185
, 185 , 200
, 250
.
Tìm độ lệch chuẩn .
Lời giải .
Nhập dữ liệu vào Statistic Calculator tại Máy tính, vẽ đồ thị, ma trận, thống kê trên Blog này
Click vào Basic Stats , đọc thống kê mô tả .
2. PHÂN PHỐI THƯỜNG -THE NORMAL DISTRIBUTION
Phân phối có biểu đồ gần đối
xứng , dạng chuông , với đa số điểm dữ liệu ở trung tâm , được gọi là phân phối thường .
Ví dụ . xem biểu đồ phân phối
sau , lưu ý đến 3
chỉ số độ đo trung tâm rất gần nhau .
Độ đo trung tâm -Measures
of Centrality
Trung bình
-Mean: 16.0020
Trung vị -Median: 16.0034
Mode: 16.0100
2.1 Biến rời rạc – biến liên
tục Discrete versus Continous Variables
- Biến gọi là rời rạc nếu có khoảng trống giữa những đữ liệu điểm khác
nhau . Ví dụ tuổi
của trẻ em trong gia đình .
- Biến gọi là liên tục nếu thể
giả sử bất kỳ giá trị nào cũng đều có thể thuộc một khoảng dữ liệu được sắp xếp
. Ví dụ chiều cao của học sinh .
Phân phối thường có 2 tính
chất chính .
1.
Tần
số của các điểm dữ liệu gần trung tâm ( hoặc trung bình ) là cao hơn tần số của
các điểm dữ liệu xa trung tâm .
2.
Phân
phối có tính đối xứng .
Vì những tính chất này nên
trung bình , trung vị và mốt hầu như gần ở trung tâm phân phối .
Ví dụ . Chiều cao của nhóm người được điều tra giả sử
có thể mô tả bởi phân phối thường . Trung bình chiều cao là 66.5 inches , độ
lệch chuẩn là 2.4 inches . Tìm và giải thích các khoảng biểu diễn cách đều 1 ,
2 và 3 độ lệch chuẩn từ giá trị trung bình . ( xem hình )
2.2 Xác suất và
diện tích -
Tìm xác suất một biến ngẫu nhiên x trong khoảng từ a đến b , ta phải xác định diện tích của hình phẳng
giới hạn từ a đến b .
2.3
Phân phối chuẩn -The Standard Normal
Distribution
Phân phối chuẩn là phân phối thường có trung bình bằng
0 và độ lệch chuẩn bằng 1 . Ta còn gọi
phân phối chuẩn là phân phối Z .
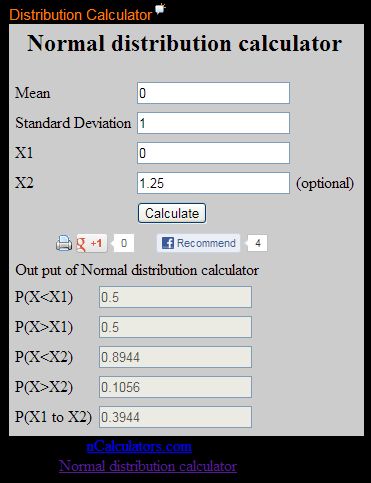
Bạn có thể sử dụng phần mềm Distribution Calculator trực tuyến dưới đây , nhập giá trị trung bình , độ lệch chuẩn , X1 , X2 và click Calculate . Đọc kết quả ở phần P(X1 to X2)
 NHẬP DỮ LIỆU Ở ĐÂY .
NHẬP DỮ LIỆU Ở ĐÂY .Distribution Calculator
**********************************************************************
b. p( z > 1.87 ) Dùng ESBPDF Analysis
Dùng phần mềm Distribution Calculator trực tuyến .
Đọc kết quả ở phần P(X > X1)
Tương tự cho các ví dụ c. và d.
2.4 Đổi sang
phân phối Z - Converting to the Z-Distribution .
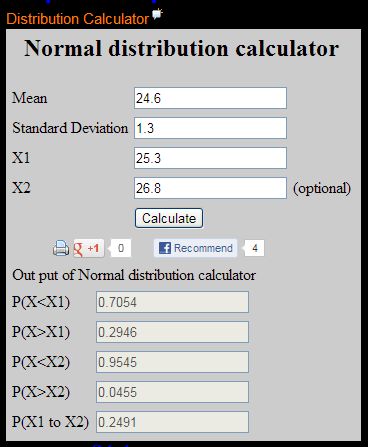
Ví dụ . Giả sử rằng tổng thể được bởi phân phối
thường có mu = 24.6 và độ lêch chuẩn sigma = 1.3 . Hỏi có bao nhiêu phần trăm dữ liệu trong
khoảng 25.3 và 26.8 ?
Dùng phần mềm Distribution Calculator trực tuyến .
Đọc kết quả ở phần P(X1 to X2)
Dùng phần mềm Distribution Calculator trực tuyến .
Đọc kết quả ở phần P(X1 to X2)
Như vậy có xấp xỉ khoảng
24.9% dữ liệu trong khoảng 25.3 và 26.8 .
Ví dụ . Chiều cao của nhóm
người Nhật được xem như có dạng phân phối thường . Trung bình chiều cao là 68 inches , độ lệch chuẩn là 4 inches . Tìm
xác suất của các biến cố sau
a. cao hơn 73 inches
b.trong khoảng 60 và
75 inches .
2.5 Biên sai - Margin
of Error ( MOE )
Ví dụ . Giả sử
rằng với độ tin cậy 90% trong chiến dịch
bầu cử , hãy tìm biên sai trong các trường hợp sau
a. kích thước mẫu n
= 275
b. kích thước mẫu n
= 750

Cách 2 : truy cập vào link sau http://www.relevantinsights.com/research-tools
Nhập liệu như hình sau , đọc MOE ( Margin of Error )
Điều này nghĩa là từ cuộc
điều tra mẫu có 275 người , ta có độ tin cậy khoảng 90% mà sai số khả dĩ lớn
nhất trong quy mô mẫu có thể cộng thêm hay bớt đi 5% điểm dữ liệu .
truy cập vào link sau http://www.relevantinsights.com/research-tools
Nhập liệu như hình sau , đọc MOE ( Margin of Error )
Ví dụ . Trong cuộc điều tra 500 sinh viên đang học tại Đại học Yale , có 410 người trả lời rằng họ sẽ tốt nghiệp sau 4 năm .
a. Tìm quy mô mẫu thỏa mãn điều kiện tốt nghiệp sau 4 năm .
b. Với độ tin cậy 95% , tìm biên sai MOE .
c. Giải thích các số liệu thu được .
Lời giải .
a. Quy mô mẫu là 410/500 = 0.82 = 82%
b.
c. Như vậy với độ
tin cậy 95% thì biên sai là 4.4% ,
khi đó quy mô mẫu sẽ là 82% + (-) 4.4% . Đây là tỷ lệ sinh viên cho rằng sẽ tốt
nghiệp sau 4 năm học .
Nói cách khác là có khoảng từ 77.6% đến 86.4% tỷ
lệ sinh viên Đại học Yale cho rằng sẽ tốt nghiệp sau 4 năm học .
3 . HỒI QUY TUYẾN TÍNH -LINEAR REGRESSION .
3.1 Công thức hồi quy tuyến tính .
3.1 Công thức hồi quy tuyến tính .
Xét hai điểm cho trước (x1,y1) và (x2,y2) , giả thiết rằng x , y có quan hệ tuyến tính , khi đó ta sẽ tìm được đường thẳng nối 2 điểm này . Quá trình tìm phương trình đường thẳng này gọi là hồi quy tuyến tính . Phương trình thỏa mãn tính chất này được gọi là mô hình toán học của quan hệ tuyến tính .
Khi các dữ liệu điểm chi ra khuynh hướng tuyến tính , ta có thể thiết lập đường thẳng xấp xỉ tốt nhất . Đường thẳng này được gọi là đường điều hóa tốt nhất ( BFL , Best-fitted Line ) .
Ví dụ : Cho các điểm (5,14),(9,17),(12,16),(14,18),(17,23)
a. Tìm đường điều hóa tốt nhất (BFL)
b. Chấm tọa độ các điểm và vẽ đồ thị của BFL trên cùng mạt phẳng tọa độ .
a. Tìm đường điều hóa tốt nhất (BFL)
b. Chấm tọa độ các điểm và vẽ đồ thị của BFL trên cùng mạt phẳng tọa độ .
Lời giải .
Xét bảng số liệu sau .
Dùng công thức tính b và a .
LƯU Ý KỸ THUẬT
Sau khi mô hình của tập hợp dữ liệu đã được tìm thấy, nó có thể được làm tròn cho mục đích báo cáo. Tuy nhiên, không sử dụng một mô hình làm tròn trong khi tính toán, và cũng không làm tròn đáp số trong quá trình tính toán, trừ khi có quy định khác. Khi mô hình được sử dụng để tìm các đáp số ngoại suy hay nội suy khác , nên được làm tròn một cách thích hợp với yêu cầu bài toán , và khi kiểm tra lại không có độ chính xác quá sai biệt so với các xuất liệu gốc .
Ví dụ * Phát tán khí thải Luợng khí thải phát tán ở Hoa Kỳ từ 1986 đến 1995 được cho ở bảng dưới đây
Năm
|
Khí thải ( tấn )
|
Năm
|
Khí thải ( tấn )
|
1986
|
109,199
|
1991
|
93,376
|
1987
|
108,012
|
1992
|
94,043
|
1988
|
115,849
|
1993
|
94,133
|
1989
|
103,144
|
1994
|
98,779
|
1990
|
100,650
|
1995
|
92,099
|
- Sắp xếp các đữ liệu với x là số năm sau 1980 và y là khối lượng khí thải phát tán ( tấn ) . Vẽ các điểm dữ liệu này .
- Viết phương trình đường điều hóa tốt nhất cho các điểm dữ liệu (BFL) .
- Vẽ đồ thị của mô hình tuyến tính trên cùng hệ trục tọa độ với các điểm dữ liệu .
- So sánh sự thay đổi của sự phát tán hằng năm và độ dốc của đường điều hóa tốt nhất BFL .
Lời giải
a. Từ 1986 đến 1995 , ta sắp xếp lại dữ liệu của x , chọn x = 0 biểu diễn cho 1980 ,
Năm
|
Khí thải ( tấn )
|
Năm
|
Khí thải (tấn)
|
6
|
109,199
|
11
|
93,376
|
7
|
108,012
|
12
|
94,043
|
8
|
115,849
|
13
|
94,133
|
9
|
103,144
|
14
|
98,779
|
10
|
100,650
|
15
|
92,099
|
Dùng CurveExpert tìm BFL .
Nhập và vẽ các điểm dữ liệu .
b. Click vào Apply Fit - > chọn Linear Fit
 |
| Thêm chú thích |
Click Info xem kết quả tìm b và a .
3.2 Hệ số tương quan tuyến tính .
Ta luôn luôn có thể tìm được BFL cho bất kỳ các tập điểm dữ liệu , nhưng độ chính xác là bao nhiêu để đường thẳng tìm được có thể đáp ứng cho mô hình toán học đó ?
Nếu những điểm dữ liệu phân tán xa BFL thì đây là quan hệ tuyến tính yếu . Ngược lại nếu chúng tập trung gần với BFL ta có mối quan hệ tuyến tính mạnh và BFL có thể đại diện cho những dự báo nội suy hoặc ngoại suy tốt .
Độ mạnh của khuynh hướng tuyến tính có thể được mô tả bởi hệ số tương quan tuyến tính , ký hiệu là r .
Một cách tổng quát , r càng gần -1 và 1 , khuynh hướng tuyến tính giữa x và y càng mạnh khi đó BFL có thể áp dụng cho dự báo một cách đáng tin cậy . Nếu r gần 0 , quan hệ tuyến tinh giữa x và y yếu đi , BFL không cho ta những kết quả dự báo tốt .
Ví dụ . Cho các diểm dữ liệu sau
(5,14),(9,17),(12,16),(14,18),(17,23) .
(5,14),(9,17),(12,16),(14,18),(17,23) .
Tìm hệ số tương quan tuyến tính r ?
Lời giải .
Ví dụ . * Thất nghiệp và thu nhập cá nhân . Bảng dữ liệu sau chỉ ra tỷ lệ thất nghiệp và tổng thu nhập cá nhân tại Hoa Kỳ theo các năm tương ứng .
- Dùng hồi quy tuyến tính để dự báo tổng thu nhập cá nhân nếu tỷ lệ thất nghiệp là 5% ( nội suy ).
- Dùng hồi quy tuyến tính để dự báo tỷ lệ thất nghiệp nếu tổng thu nhập cá nhân là $10 billion ( 10 tỷ USD ) ( ngoại suy ) .
- Những dự báo ở câu (a) và (b) có đáng tin cậy không ? Giải thich ?
Năm
|
Tỷ lệ thất nghiệp
( % )
|
Tổng thu nhập cá nhân
(Tỷ $USD )
|
1975
|
8.5
|
1.3
|
1980
|
7.1
|
2.3
|
1985
|
7.2
|
3.4
|
1990
|
5.6
|
4.8
|
1995
|
5.6
|
6.1
|
2000
|
4.0
|
8.3
|
Lời giải
- Nhập và vẽ các điểm dữ liệu bằng Curve Expert với x là tỷ lệ thất nghiệp , y là tổng thu nhập .
Linear fit để tìm các hệ số của BFL .
c. Với hệ số tương quan tuyến tính r = -0.970438 sát với -1 , có thể kết luận những dự báo này là có độ tin cậy tốt , quan hệ tuyến tính giữa x và y có mức độ mạnh .
Ngoài ra , vì r <0 , ta có thể nói rằng tổng thu nhập cá nhân y ( total personal income ) giảm dần khi tỷ lệ thất nghiệp x ( unemployment rate ) gia tăng .
Trần hồng Cơ
30/10/2012

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
-------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
Pure mathematics is, in its way, the poetry of logical ideas.
Albert Einstein .