GIỚI THIỆU VỀ PHƯƠNG TRÌNH VI PHÂN .
Chương 4-
PHẦN 1 .
Phương trình vi phân tuyến tính cấp cao với hệ số hằng .
Phương pháp hệ số bất định .
Phương pháp biến thiên tham số .
Bài tập thực hành .
Loạt bài sau đây giới thiệu về phương trình vi phân một cách tổng quan , các khái niệm cơ bản và phương pháp giải được trình bày tinh giản dễ hiểu . Bạn đọc có thể sử dụng các phần mềm hoặc công cụ online trích dẫn chi tiết trong bài viết này để hỗ trợ cho việc học tập và nghiên cứu . Ngoài ra tác giả cũng sẽ đề cập đến những ví dụ minh họa cụ thể , các mô hình thực tế có ứng dụng trong lĩnh vực phương trình vi phân .
Trần hồng Cơ .
12/04/2013 .
****************************************************************************

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
1. Tổng quan về phương trình vi phân tuyến tính cấp cao .
1.1 Các khái niệm cơ bản .
Chúng ta đã đề cập đến phương trình vi phân tuyến tính cấp 2 gồm những khái niệm về hệ cơ sở , định thức Wronski và nguyên lý chồng chất nghiệm trong Chương 2 - Phần 1 . 3 .
Tiếp tục ở chương 4 tác giả sẽ trình bày tóm tắt các cách giải cho phương trình vi phân cấp cao thông qua ví dụ .
1.1.1 Dạng tổng quát .
Ví dụ 1 .
Ký hiệu .
Đạo hàm cấp k theo biến x của hàm số y ( khả vi liên tục đến cấp k ) được ký hiệu
Khi đó ta nói D là toán tử vi phân ( xem Chương 2 - Phần 4 . 1 và 2 ) . Dạng tổng quát của phương trình vi phân tuyến tính theo toán tử như sau
Ví dụ 2 .
1.1.2 Tính chất của toán tử vi phân .
1.2 Công thức .
Một số công thức toán tử vi phân được áp dụng cho việc tìm nghiệm phương trình vi phân tuyến tính .
1.2.1 Toán tử vi phân và hàm mũ .
Cho P(t) là đa thức theo biến t với các hệ số hằng ak , có dạng
khi thay biến t bằng toán tử vi phân D ta có
Quan hệ giữa toán tử vi phân và hàm mũ .
* Tương tự xét P(x, t) là đa thức theo biến t với các hệ số là hàm ak (x) , có dạng
thay biến t bằng toán tử vi phân D ta có
1.2.2 Định lý cơ bản .
Giả sử u(x) là một nghiệm riêng của phương trình vi phân tuyến tính (1)
P(x,D)(y) = R(x) ,
và v(x) là nghiệm của phương trình thuần nhất P(x,D)(y) = 0 , khi đó y = u(x) + v(x) là nghiệm tổng quát của (1) .
* Dựa vào định lý này chúng ta đưa ra phương pháp tìm nghiệm tổng quát của (1) như dưới đây
+Tìm nghiệm thuần nhất của (1) yTN = v(x) .
+Tìm nghiệm riêng của (1) yR = u(x) .
Nghiệm tổng quát của (1) có dạng :
yTQ = yTN + yR
Từ phương trình thuần nhất P(x,D)(y) = 0 , ta giả thiết rằng P(x,D) độc lập x , i.e các hệ số ak là hằng . Với
2. Phương trình vi phân tuyến tính cấp cao với hệ số hằng .
Xét phương trình vi phân tuyến tính cấp cao hệ số hằng
P(D)(y) = R(x) (2)
Phương trình đặc trưng tương ứng là
P(m) = 0 .
2.1 Nghiệm thuần nhất .1.2 Công thức .
Một số công thức toán tử vi phân được áp dụng cho việc tìm nghiệm phương trình vi phân tuyến tính .
1.2.1 Toán tử vi phân và hàm mũ .
Cho P(t) là đa thức theo biến t với các hệ số hằng ak , có dạng
khi thay biến t bằng toán tử vi phân D ta có
Quan hệ giữa toán tử vi phân và hàm mũ .
* Tương tự xét P(x, t) là đa thức theo biến t với các hệ số là hàm ak (x) , có dạng
thay biến t bằng toán tử vi phân D ta có
1.2.2 Định lý cơ bản .
Giả sử u(x) là một nghiệm riêng của phương trình vi phân tuyến tính (1)
P(x,D)(y) = R(x) ,
và v(x) là nghiệm của phương trình thuần nhất P(x,D)(y) = 0 , khi đó y = u(x) + v(x) là nghiệm tổng quát của (1) .
* Dựa vào định lý này chúng ta đưa ra phương pháp tìm nghiệm tổng quát của (1) như dưới đây
+Tìm nghiệm thuần nhất của (1) yTN = v(x) .
+Tìm nghiệm riêng của (1) yR = u(x) .
Nghiệm tổng quát của (1) có dạng :
yTQ = yTN + yR
Từ phương trình thuần nhất P(x,D)(y) = 0 , ta giả thiết rằng P(x,D) độc lập x , i.e các hệ số ak là hằng . Với
2. Phương trình vi phân tuyến tính cấp cao với hệ số hằng .
Xét phương trình vi phân tuyến tính cấp cao hệ số hằng
P(D)(y) = R(x) (2)
Phương trình đặc trưng tương ứng là
P(m) = 0 .
Nghiệm của phương trình vi phân tuyến tính cấp cao thuần nhất hệ số hằng
P(D)(y) = 0
gọi là nghiệm thuần nhất .
2.1.1 Công thức của nghiệm thuần nhất .
a. Phương trình đặc trưng có nghiệm thực - riêng biệt .
+Khi P(m) = 0 có n nghiệm thực mk , k = 1,..,n riêng biệt .
Nghiệm thuần nhất là
+Khi P(m) = 0 có k nghiệm phức mk , k = 1, 2,...
Nghiệm thuần nhất là

c. Phương trình đặc trưng có nghiệm bội .
+Khi P(m) = 0 có nghiệm thực bội cấp p là mp
Nghiệm thuần nhất tương ứng
+Khi P(m) = 0 có nghiệm phức bội cấp p là mp
Nghiệm thuần nhất tương ứng
2.1.2 Các ví dụ minh họa .
Ví dụ 1 . Tìm nghiệm thuần nhất của các phương trình vi phân tuyến tính cấp cao hệ số hằng sau đây .
Lời giải .
a. nghiệm thực-rời .
b.nghiệm thực -rời .
c.nghiệm phức.
d.nghiệm phức.
Bổ sung về số phức .

Lời giải .
e.nghiệm phức -căn bậc n.
Từ phương trình đặc trưng , áp dụng công thức căn bậc n của số phức .

Lời giải .
g.nghiệm thực-bội cấp p .
h.nghiệm thực-bội cấp p.
i.nghiệm thực-bội cấp p.
k.nghiệm phức-bội cấp p.
Khảo sát một số phương trình vi phân tuyến tính cấp cao hệ số hằng có nghiệm phức -bội cấp p như sau .
Ví dụ 4 .
l.nghiệm phức-bội cấp p .

Các nghiệm phức-bội cấp 2 là :
hay
m.nghiệm phức-bội cấp p .

Các nghiệm thực-bội và phức-bội cấp 2 là :

Các nghiệm thực-bội và phức-bội cấp 2 là :
Các nghiệm thực-rời , thực-bội và phức-bội cấp 2 là :
Nghiệm thuần nhất có dạng
p.Nghiệm thực-bội và phức-bội cấp p1 , p2 .
Các nghiệm thực-bội cấp 3 , cấp 2 và phức-bội cấp 2 là :
2.2 Nghiệm riêng và nghiệm tổng quát .
+Nghiệm đặc biệt thỏa mãn phương trình vi phân tuyến tính cấp cao không thuần nhất hệ số hằng
P(D)(y) = R(x) (2)
gọi là nghiệm riêng , ký hiệu là yR .
+Nghiệm tổng quát của phương trình vi phân tuyến tính cấp cao có dạng
yTQ = yTN + yR
Trong đó yTN là nghiệm thuần nhất của phương trình vi phân tuyến tính cấp cao .
3. Phương pháp hệ số bất định tìm nghiệm riêng ( Undetermined Coefficients ) .
3.1 Công thức .
Để tìm nghiệm riêng cho phương trình vi phân tuyến tính cấp cao
P(D)(y) = R(x) (2)
ta dựa vào vế phải của (2) , chọn hàm tương ứng với các hệ số bất định . Muốn tìm các hệ số này ta thay nghiệm riêng vào phương trình , thực hiện đồng nhất hệ số hai vế để tìm được hệ phương trình chứa các hệ số đó ( Xem thêm ở Chương 2-Phần 4 - 4 ) .
3.2 Ví dụ minh họa .
Ví dụ 5 .
Tìm nghiệm riêng và nghiệm tổng quát của các phương trình sau
Lời giải .
a. vế phải R(x) là hàm mũ , xét phương trình thuần nhất
Đồng nhất hệ số hai vế , ta có
5C = 1/2 => C = 1/10
Nghiệm tổng quát của phương trình là
b. vế phải R(x) là hàm hỗn hợp đa thức-mũ , xét phương trình thuần nhất
Đồng nhất hệ số hai vế , ta có
{ 8A = 1 , 3A + 4B = 0 }=> A = 1/8 , B = -3/32 .
Nghiệm tổng quát của phương trình là
c. vế phải là một tổng gồm hàm đa thức và lượng giác , xét phương trình thuần nhất .
Trường hợp thứ nhất với vế phải là hàm đa thức , tìm nghiệm riêng yR2
Nghiệm tổng quát của phương trình như sau
d. vế phải R(x) là tích hàm mũ và lượng giác, xem lại Chương 2-Phần 2 . a (ii) và b. ví dụ 2 c.
Thủ tục tính toán cách 1 .

+Tìm nghiệm của phương trình đặc trưng và tìm dạng nghiệm phức .
Thủ tục tính toán cách 2 .
+Tìm nghiệm thuần nhất của phương trình
+Tìm nghiệm riêng của phương trình với dạng sau
thay vào phương trình không thuần nhất , đồng nhất hệ số ta có
Nghiệm tổng quát của phương trình như sau
4. Phương pháp biến thiên tham số tìm nghiệm riêng ( Variation of Parameters ) .
4.1 Nghiệm riêng của phương trình vi phân tuyến tính cấp 2 .
Để tìm nghiệm riêng cho phương trình vi phân tuyến tính cấp cao
P(D)(y) = R(x) (2)
ta có thể áp dụng phương pháp biến thiên tham số ( xem Chương 2-Phần 2 . 2.3 ) .
Như đã trình bày trong phần trước đó , phương pháp biến thiên tham số không cần các điều kiện đầu hoặc dạng của hàm R(x) và hoàn toàn chỉ phụ thuộc vào phép tính tích phân .
+Trường hợp đơn giản nhất là xét phương trình vi phân cấp 2 tuyến tính hệ số hằng không thuần nhất
Với { y1(x) , y2(x) } là hệ cơ sở của phương trình cấp 2 tuyến tính hệ số hằng thuần nhất . Khi đó
yTN = C1y1(x) + C2y2(x)
Ý tưởng chính của phương pháp biến thiên tham số là đi tìm biểu thức nghiệm riêng có dạng
yR = u1(x)y1(x) + u2(x)y2(x)
Tính các đạo hàm cấp 1 và cấp 2 của nghiệm riêng :
Ta có định thức Wronski ( Xem Chương 2 - Phần 1- 3.2 b.)
Tóm tắt .
4.2 Các ví dụ minh họa .
Ta sẽ khảo sát lại các ví dụ ở Chương 2-Phần 2 . 2.3 đối với các phương trinh vi phân tuyến tính cấp 2 hệ số hằng , từ đó đưa ra phương pháp tổng quát cho phương trình vi phân tuyến tính cấp cao .
Ví dụ 6 . Giải các phương trình vi phân sau
Ví dụ 7 . Giải các phương trình vi phân sau
Trong phần này ta sẽ theo dõi cách giải của bài toán b. và c. tương ứng với phương trình vi phân tuyến tính cấp 3 .
b. Xét phương trình vi phân
+Tìm nghiệm thuần nhất
+Nghiệm riêng cần tìm có dạng
+Thiết lập hệ phương trình tuyến tính
+Giải hệ này bằng Maple , tìm u1(x) , u2(x) và u3(x) .
+Hệ nghiệm { u1(x)' , u2(x)' , u3(x)' } thu được là
+Tích phân lên ta có hệ { u1(x) , u2(x) , u3(x) } và nghiệm RIÊNG của phương trình sẽ có dạng
* Lưu ý :
-Nhờ vào công cụ đại số tuyến tính , việc tìm các nghiệm cơ sở { u1(x) , u2(x) , ... , uj(x) } sẽ đơn giản hóa và ta thu được nghiệm riêng của phương trình vi phân tuyến tính cấp cao .
-Tuy vậy phương pháp biến thiên tham số cũng có nhược điểm là khi tích phân hệ { u1(x)' , u2(x)' , ... , uj(x)' } nhưng không có được kết quả dạng hiển của { u1(x) , u2(x) , ... , uj(x) } thì nghiệm RIÊNG của phương trình sẽ chứa biểu thức tích phân .
c.Ví dụ sau đây cho ta biểu thức nghiệm riêng ở dạng tích phân . Xét phương trình vi phân
+Tìm nghiệm thuần nhất
+Thiết lập hệ phương trình tuyến tính
+Từ hệ nghiệm { u1(x)' , u2(x)' , u3(x)' } , tích phân theo biến x , ta có
+Nghiệm RIÊNG và tổng quát của phương trình sẽ có dạng tích phân .
4.3 Phương pháp chung .
Từ 2 bài toán b. và c. đã xét , ta có thể đưa ra phương pháp tổng quát cho phương trình vi phân tuyến tính cấp cao như sau .
+Tìm nghiệm thuần nhất yTN của phương trình bằng các công thức 2.2.1 .
5. Bài tập thực hành .
28/04/2013 .
 This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.-------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
Pure mathematics is, in its way, the poetry of logical ideas.
Albert Einstein .






































































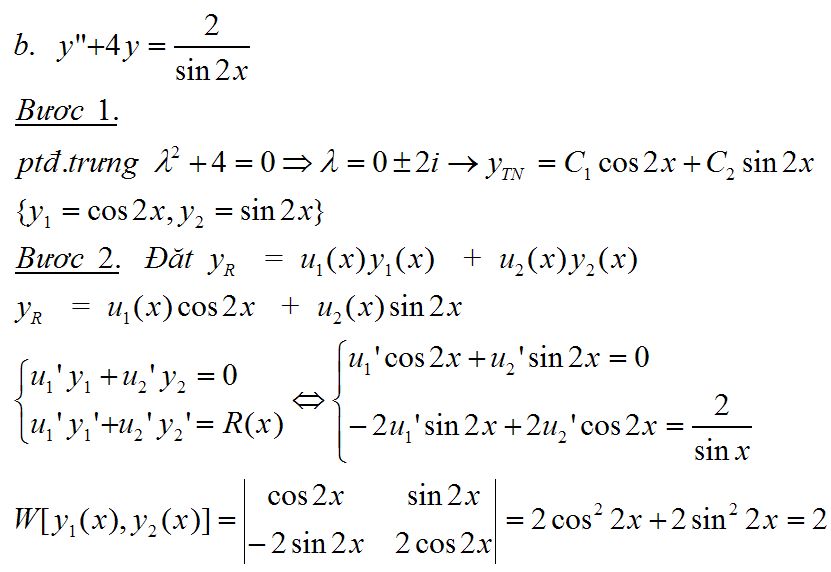























Không có nhận xét nào:
Đăng nhận xét
Cám ơn lời bình luận của các bạn .
Tôi sẽ xem và trả lời ngay khi có thể .
Thank you for your comments.
I will review and respond to these issues as soon as possible.
Trần hồng Cơ .
Co.H.Tran
MMPC-VN
cohtran@mail.com