
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
TOÁN THỰC HÀNH CHƯƠNG 2 . 2.3
Bài
giảng .
2. 3 TÀI
CHÍNH CƠ BẢN .
Chủ đề
- Tiền lãi .
- Lợi tức đồng niên-Tiền góp hằng năm (Annual yield –annuity) .
- Khoản vay (Loans) .
Ứng dụng
- Vay mượn (Borrowing) .
- Khoản góp hằng tháng (Monthly payment) .
- Kết số (Future value) .
- Thực số (Present value) .
Khái niệm cơ bản
* Tiền lãi ( Lãi đơn
-Simple –Lãi kép- Compound – Lãi trả góp -Add -on interest
) .
* Lợi tức đồng niên – Tiền góp hằng năm – Quỹ chìm (Annual yield
-Annuity –Sinking fund ).
* Khoản vay -Loans
( Vay trả góp -Amortized Loan –Lịch trả góp-Amortized schedule - APR )
1. TIỀN LÃI - INTEREST
Số tiền ban đầu cho vay được
gọi là vốn hoặc thực số . Nếu một số vốn đã được trả lại, sau đó là phần còn lại
chưa thanh toán được gọi là dư nợ gốc, hoặc tài khoản có . Tổng số tiền cho vay
được trả lại được gọi là kết số , bao gồm số tiền ban đầu cho vay và lợi nhuận
hoặc tiền lãi của người cho vay . Tiền lãi sẽ được thanh toán phụ thuộc vào tỷ lệ
lãi suất.
1.1 Lãi đơn - Simple
interest
Lãi đơn I tính
trên vốn P theo lãi suất định kỳ năm r với số năm t là
I = P r
t
Kết số FV của
vốn P
lãi suất định kỳ năm r với số năm t là
FV = P (
1 +
r t )
Ví dụ . Cửa hàng tạp hóa ABC đã vay $340,000
lãi suất định kì năm 5.1% trong
120 ngày để mua hàng mùa Giáng sinh . Tìm
tiền lãi phải trả ?
Lời giải .
Ta có vốn P =
340,000 lãi suất r =
5.1% = 0.051
1
năm --- 365 ngày
t?
năm --- 120 ngày
Thời
gian
t
= 120 ngày =
120/365 ( năm)
I = P r
t = 340,000 x 0.051 x 120/365 =
5700.8219 » $5700.82
Ví dụ . Để trả tiền nhập hàng , Cửa hàng tạp hóa ABC đã vay $185,000 lãi suất
năm 7.3% trong 4 tháng . Tìm kết số FV của khoản vay .
Lời giải .
Ta có vốn P = $185,000 ,
lãi suất năm r = 7.3%
= 0.073
1
năm --- 12 tháng
t?
năm --- 4 tháng
Thời gian 4 tháng = 4/12 năm
Áp dụng FV = P ( 1
+ r t )= 185,000 x 0.073 x 4/12 = 189501.6667
» $189501.67 .
Điều này nghĩa là cửa hàng
ABC phải trả $185,000 cộng thêm $4501.67 tiền lãi vào cuối
kỳ vay 4 tháng .
Ví dụ . Tìm số vốn cần đầu
tư hiện nay ( present value -thực số ) với lãi suất 0.0575 để thu
được $1000 trong 2 năm .
Lời giải .
FV = P ( 1
+ r t ) hay
P = FV/ ( 1 + r t )
P = FV/ ( 1 + r t )
Ta có
FV = 1000
; r =
0.0575 ; t
= 2
hay P = 1000 / ( 1
+ 0.0575 . 2 ) = 896.86
Vậy vốn đầu tư hiện nay ( thực số )
là $896.86
1.2 Lãi trả góp - Add-on
interest
Lãi đơn có kết số được chia đều thành mỗi kỳ
trả bằng nhau ta gọi là lãi trả góp , kí hiệu
AoI
Ví dụ . Eddie mua một laptop trị giá $1,300
ở Wall-Mart . Anh ấy trả trước $200 và chấp thuận trả góp với lãi suất 10% lãi trả dần trong 2 năm . Tìm số tiền trả góp hằng tháng .
Lời giải .
P = khoản
vay = 1,300 -
200 = 1,100 ($) ;
Lãi suất r = 0.1
; thời gian t =
2 (yrs)
Vậy FV = P (
1 +
r t ) = 1,100 . ( 1 + 0.1 x 2 ) =
1,320 ($)
AoI
= FV / t = 1,320 / 24 = $55/
tháng .
1.3 Công thức lãi kép -Compound Interest Formula
Tại cuối mỗi n kỳ , kết số của vốn ban đầu P
tính theo lãi kép với lãi suất r định kỳ năm và t là thời gian (năm) . Ta có
Trong đó
r lãi suất định kỳ năm ( the annual interest
rate)
i lãi suất định kỳ ( the periodic interest rate ) = r . t
n là số kỳ
.
I tiền
lãi ( the interest) .
Ví dụ . Với
số vốn $1,000 gửi vào tài khoản với 8%
lãi kép định kỳ quí (interest compounded
quartly) . Tìm kết số ( FV ) sau 6 tháng .
+ Tính theo công thức lãi đơn :
Vì lãi kép định kỳ quí , tiền lãi sẽ được tính và tích lũy vào vốn ban đầu mỗi quí .
Cuối quí thứ nhất ta có ,
P = 1,000 ,
r = 0.08 , t = ¼
FV = P (
1 +
r t ) = 1000( 1 + 0.08x1/4 ) =
1020
Cuối quí
thứ nhất ta có ,
P
= 1,020 , r = 0.08 , t = ¼
FV = P (
1 +
r t ) = 1020( 1
+ 0.08x1/4 ) = 1040.40
+ Tính
theo công thức lãi kép :
1 năm --- 4
quí
t? năm --- 1
quí => t = ¼ năm
Lãi suất định kỳ i
= r . t = 0.08 x ¼
= 0.02 ,
1 kỳ ( quí ) ---
3 tháng
n kỳ ? ---
6 tháng => n = 2 kỳ
áp dụng công thức lãi kép
Ví dụ .
a. Tìm kết số FV của khoản
vốn $2,000 gửi vào tài khoản lãi suất
10.3% định kỳ ngày trong 15 năm .
b. Tìm tiền lãi thu được .
Lời giải .
Ví dụ .
a. Tìm kết số FV của khoản
vốn $2,500 gửi vào tài khoản lãi suất
10.3% định kỳ ngày trong 15 năm .
b. Tìm tiền lãi thu được .
Lời giải .
a. Lãi kép định kỳ ngày :
P = 2,500 ,
r = 10.3% = 0.103
,
1 năm --- 365 ngày
t ? năm ---
1 ngày
thời gian t = 1/365
Lãi suất định kỳ i = r . t
= 0.103 x( 1/365 )
365 kỳ (ngày) ---
1 năm
n kỳ ? --- 15 năm => n
= 15 x 365 = 5,475 kỳ
áp dụng công thức lãi kép
b. Vốn là
$2,500 và kết số FV là $11,717.37
, vậy tiền lãi thu được = Kết số (FV)
- Vốn (P) = 11,717.37 - 2,500 = 9,217.37 ($)
Dưới đây là bảng so sánh từng năm giữa lãi
đơn , lãi kép định kỳ năm , quí , tháng và ngày với cùng một khoản vốn $1000 ,
cùng lãi suất 10% và cùng kỳ 10 năm .
2. LỢI TỨC ĐỒNG
NIÊN – TIỀN GÓP HẰNG NĂM ( ANNUAL YIELD
- ANNUITY )
2.1 Lợi tức đồng niên - Annual yield
Lợi tức đồng niên của khoản tiền gửi lãi suất
kép là lãi suất đơn có cùng một kết số với lãi suất kép đó thu được trong 1 năm
. Tìm lợi tức đồng niên bằng cách giải phương trình sau tìm r .
Ví dụ . Tìm lợi tức đồng niên của $2500 gửi vào tài
khoản lãi kép 10.3% định kỳ ngày trong
15 năm .
Lời giải .
Ví dụ . Tìm lợi tức đồng niên tương ứng với lãi suất
ấn định là 8.4% lãi kép định kỳ tháng (compounded
monthly) .
Lời giải .
Tính lãi kép trong 1 năm
Vậy lợi tức đồng niên là 8.73%
2.2 Tiền góp hằng năm - Annuity
Tiền góp hằng năm là dãy những khoản góp đều đặn bằng nhau
vào tài khoản trong đó mỗi khoản đóng nhận một lãi suất kép .
Ví dụ . Đóng $50 hàng tháng với lãi suất 10% .
Tính kết số thu được trong 40
năm với :
a. Lãi đơn .
b. Lãi kép định kỳ tháng .
Lời giải .
a.
Lãi
đơn : $50 x tháng x 40 năm = $24,000
b.
Lãi
kép :
t = 1/12
i =
r. t =
0.1x 1/12 = 0.0083
n
= 40 x 12 = 480 kỳ
* Kết số FV
của tiền góp hằng năm thông thường với khoản góp pymt = $50 , lãi suất định kỳ i = 0.1/12
, và n = 480 lần đóng là :
$ 316,204 * Kết số FV của tiền góp hằng năm đáo hạn với khoản góp pymt = 50$ , lãi suất định kỳ i = 0.1/12 , và n = 480 lần đóng là :
$318,839
2.3 Quỹ chìm -
Sinking Fund là khoản góp hằng năm được
tiết kiệm dùng vào mục đích cá nhân nào đó .
Ví dụ . Jack và Anna muốn lập một quỹ chìm dành cho
việc học tập của đứa con của họ . Biết quỹ này có tài khoản tiền góp hằng năm
thông thường , để có ngân quỹ $30,000 trong 18 năm , lãi suất 9¼ % lãi kép định kỳ 2 tuần , họ phải đóng tiền
góp mỗi kỳ là bao nhiêu ?
Lời giải .
Từ
công thức
tiền góp mỗi kỳ ( 2 tuần ) là $24.9950 ~ $25 .
Ví dụ . Lấy ví
dụ như trên . Hãy tính
a. Kết số thực của quỹ chìm .
b. Số tiền thực đóng của Jack và Anna .
c. Tổng tiền lãi của quỹ chìm .
Lời
giải .
a. Như đã biết pymt =
$25 ,
i = r.t =
0.0925´1/26 ; n = 18
´ 26 = 468
Từ
công thức
Kết số thực của quỹ chìm là $30,000.95
b. Số tiền thực đóng của Jack và Anna là :
468 kỳ x $25/kỳ = $11,700 .
c. Tổng tiền lãi của quỹ chìm = FV - Số tiền thực đóng
= $30,005.95 – $11,700 = $18,305.95
2.4
Tiền góp hằng năm hoãn thuế -
Tax-Deferred Annuity ( TDA )
Là khoản tiền góp hằng
năm dành cho hưu trí .
Ví dụ . Paul .K
vừa tìm được công việc mới , anh
ta muốn lập một quỹ hưu trí TDA . Paul mở một tài khoản tiền góp hàng năm thông
thường bằng cách đóng $200 / tháng , lãi suất 8¾ % , lãi kép định kỳ tháng .
a.
Tìm kết số FV của
quỹ TDA trong 35 năm sau .
b.
Tìm tiền lãi
của quỹ TDA này .
kết số FV của quỹ TDA trong 35 năm sau là $552539.95 ~ $552,540
b .Tiền lãi của quỹ TDA này = Kết số FV - số tiền thực đóng =
$552,540 - $200 x 420 = $468,540
3. KHOẢN VAY - LOANS
3.1 Vay trả
góp - Amortized Loan là khoản
vay mà vốn vay và lãi được trả thành nhiều đợt định kỳ với một khoản bằng nhau
.
Trong đó pymt
là khoản trả góp , i là lãi suất định kỳ (periodic interest rate ) ,
n là số kỳ (number of periods ) ,
P là thực số ( Present Value - PV) hay
là tổng món nợ .
Công thức này dùng để xác định 1 trong số 4 tham
số { pymt
, i, n , P } nếu có 3 tham số kia
.
Ví dụ . George mua
chiếc xe hơi trị giá $13,518.77 . Anh ta
trả trước $1,000 và vay trả góp lãi đơn 4-năm
từ US Bank với lãi suất 12% định kỳ tháng . Tìm các khoản sau
a. Khoản góp phải trả hằng tháng .
b. Tổng tiền lãi của khoản vay .
Lời
giải .
a. Các tham số cho trước :
P = khoản vốn vay = 13,518.77 - 1,000 =
12,518.77 $
r =
12% =
0.12 ; i = r.t =
0.12 x 1/12
n
= 4 x 12 ( kỳ )
Tìm pymt ?
Từ công thức

Khoản góp phải trả hằng tháng là $329.67 ( gồm vốn vay và lãi - principal and interest )
b. George
trả 48 kỳ với $ 329.67 / kỳ
Nên tổng số tiền phải trả
là :
48 x 329.67 $ = $15824.16
Tổng
tiền lãi của khoản vay = tổng số tiền phải trả – vốn vay
= $15824.16
- $12,518.77
= $3,305.39
3.2 Lịch trả
góp - Amortization Schedule . Mỗi khoản trả góp bao gồm vốn vay và lãi . Lịch trả
góp là một bảng kê các kỳ trả góp trong đó chỉ ra tiền vốn vay , phần lãi và số tiền còn lại phải trả sau mỗi kỳ hoàn tất trả góp ( số dư nợ ).
Ví dụ . Với ví dụ như trên ta thiết lập lịch trả góp
cho khoản vốn vay trả góp lãi đơn 4-năm của George trong 4 tháng đầu tiên .
Lời giải .
Khoản vốn vay là $12,518.77 , trả góp trong 48 tháng . Tiền
góp tháng là $329.67 .
Ta có r =
12% = 0.12 ,
t = 1 tháng = 1/12 (năm) ,
P =12,518.77 .
*Kỳ 1 : Tiền lãi đơn I
= Prt =
12,518.77 x 0.12 x 1/12 = 125.1877 ~ $125.19
Trả vốn kỳ 1 : $329.67
- $125.19 = $204.48
( vốn = tiền góp – lãi )
Số dư nợ còn lại phải trả
$12,518.77 -
$204.48 = $12,314.29
*Kỳ 2 : Tiền lãi đơn I = Prt =
12,314.29 x 0.12 x 1/12 = 123.1429 ~ $123.14
Trả vốn kỳ 2 : $329.67
- $123.14 = $206.53
(vốn = tiền góp – lãi )
Số dư nợ còn lại phải trả
$12,314.29 - $206.53 =
$12,107.76
*Kỳ 3 : Tiền lãi đơn I = Prt =
12,107.76 x 0.12 x 1/12 =
121.0776 ~ $121.08
Trả vốn kỳ 3 : $329.67
- $121.08 = $208.59
(vốn = tiền góp – lãi )
Số dư nợ còn lại phải trả
$12,107.76 -
$208.59 = $11899.17
*Kỳ 4 : Tiền lãi đơn I = Prt =
11899.17 x 0.12 x 1/12 = 118.9917
~ $119
Trả vốn kỳ 4 : $329.67
- 119$ = $210.67
(vốn = tiền góp – lãi )
Số dư nợ còn lại phải trả
$11899.17 -
$210.67 = $11688.5
Dưới đây là một đoạn Maple code , tác giả đã soạn thảo cho việc tính khoản tiền góp và lịch trả góp ( ver 6.0 )
> restart; with(finance);
> eqPRESENTVALUE:=P*(1+i)^n=Pymt*((1+i)^n-1)/i:solve(eqPRESENTVALUE,{Pymt});n:=48;i:=0.12/12;P:=12518.77;; ;PV:=solve(eqPRESENTVALUE,{Pymt});
Hướng dẫn :
Trong phần này vốn vay P = 12518.77 , số kỳ n = 48 ( 4 năm , mỗi năm 12 kỳ ) , lãi suất định kỳ i = r.t = 0.12 /12
ta tìm được pymt = 329.667
Hướng dẫn :
Nhập khoản vốn vay P = 12518.77 khoản
khoản tiền góp 329.667 và i = r.t = 0.12 /12
vào đoạn code sau
> A:= amortization(12518.77,329.667, 0.12/12);
> amortization_table[n, Payment, Interest, Principal, Balance] = matrix(A[1]);
Đoạn code này sẽ tính kỳ và tạo lịch trả góp , phần số liệu trong khung đỏ chỉ ra lịch trả góp của George trong 4 tháng đầu tiên .
Bạn có thể dùng công cụ trực tuyến tại
 http://www.javascriptsource.com/repository/javascripts/2003/03/111241/interest.html
http://www.javascriptsource.com/repository/javascripts/2003/03/111241/interest.htmlNhập số liệu như hình sau và click Compute .
hoặc truy cập :

http://www.javascriptsource.com/repository/javascripts/1999/02/26/JS_17387/script17387.html
Nhập số liệu như hình sau và Click Monthly Payment để biết tiền góp hằng tháng ; Click Amortize This để xem lịch trả góp .
Kết quả như sau

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.
-------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
Pure mathematics is, in its way, the poetry of logical ideas.
Albert Einstein .





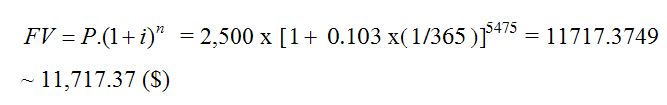






















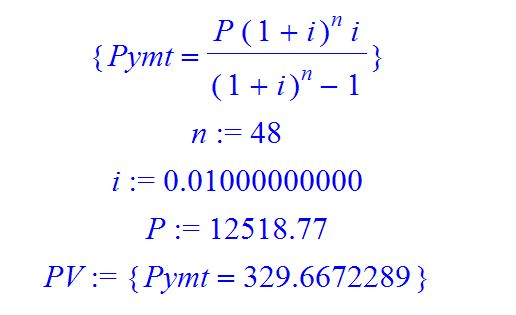







Không có nhận xét nào:
Đăng nhận xét
Cám ơn lời bình luận của các bạn .
Tôi sẽ xem và trả lời ngay khi có thể .
Thank you for your comments.
I will review and respond to these issues as soon as possible.
Trần hồng Cơ .
Co.H.Tran
MMPC-VN
cohtran@mail.com