TOÁN THỰC HÀNH CHƯƠNG 1 . 1.1

This work is licensed under a
 Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

Đây là tài liệu  môn Mathematics dành cho sinh viên chuyên ngành Quản trị kinh doanh của chương trình  Du học tại chỗ - Liên kết đào tạo với Đại học Hoa kỳ , tác giả đã trực tiếp biên soạn và giảng dạy các năm 2008-2010 . ( Xem đề cương chi tiết tại  http://cohtran.yolasite.com/semester-courses.php )

Bản gốc giáo trình này bằng tiếng Anh , được dịch và chỉnh lý sang Việt ngữ với tựa đề TOÁN ĐƠN GIẢN - TOÁN HỌC THỰC HÀNH  với ý định rõ ràng : đó là cung cấp cho người đọc những khái niệm Toán học cùng các ứng dụng trong thực tế .

Như tên gọi của nó , thật hết sức đơn giản khi làm việc với những định nghĩa , định lý , hệ quả và đặc biệt là việc vận dụng linh hoạt các nội dung này vào những hoạt động khoa học-kinh tế -xã hội , nhận biết được các lợi ích cũng như những dự báo có tính chính xác tương đối cao .

Rất mong nhận được nhiều đóng góp tích cực từ người đọc để bản thảo này được hoàn thiện hơn .

Xin liên lạc với tác giả qua e-mail : cohtran@mail.com

Trần hồng Cơ ,

Ngày 19/06/2012 .

COURSE SYLLABUS

MATHEMATICS

Lecturer : MSc Math-Mech TRAN HONG CO .

Introduction

The goal of this course is to expose students to topics in Mathematics that are often used in scientific approaches especially in economic and business management . The mathematic course contains many problems from the basic to the advanced, to supply student with  a wide range of abilities and interests. Beside some of the examples are simply designed to build skills, every effort has been made to generalize problems, so that students can see common uses and practical applications of the mathematics they are studying, and appreciate the power of mathematics. We hope that students will be able to seize the essence of all the matters and also make use of mathematical concepts to the realities .  

Objectives

There are three objectives  :

1  .To introduce the basic concepts in mathematics : sets , counting and logic . From the such essentials , the students would be provided knowledge to access data with combinatorics , probability and financial tools .

2  . Considering the operations        and applications of matrices  . The students would be communicated key concepts in linear algebra and usefulness of matrices for solving the optimization problem and prediction by Markov’s chains .

3  . To provide the concepts in calculus and applications to the students briefly but completely including limitation , differentiation and integration . 

Materials

Students can refer to materials as following

-Mathematics – A practical course , CoHongTran , 2008

-Mathematics for the international student , Paul Urban , Haese-Harris

Publications , 2004 .

-Calculus I , Paul Dawkins , 2007 . -Business Calculus Demystify , Rhonda HuettenMueller , Mc Graw-

Hill , 2006 .

-Mathematics –A practical Odyssey , David B. Johnson , Thompson-Brooks/Cole , 2005 .

Contents

Mathematics is a 16-week course , including 7 chapters , 5 home assignments , a midterm and final test . 

Chapter 1 . LOGIC , SETS  AND COUNTING

1.1 SETS – BINARY OPERATIONS

1.2 SYMBOLIC LOGIC – BICONDITIONAL

1.3 COUNTING - COMBINATORIAL LOGIC

 Chapter 2 . PROBABILITY , STATISTICS AND FINANCE .

2.1   PROBABILITY - COMBINATORICS –EXPECTED  VALUE

2. 2 STATISTICS , LINEAR REGRESSION  

2. 3 FINANCE

    

                   

Chapter 3 . GEOMETRY

3.1 GEOMETRICAL FORMULAS

3.2 POLYGON GEOMETRY

3.3 SPACE SOLID GEOMETRY

3.4 2D AND 3D COORDINATE SYSTEMS

3.5 TRIGONOMETRY 

3.6 CONIC

   

                    

Chapter 4 . LINEAR ALGEBRA

4.1 MATRICES – BASIC OPERATIONS

4.2 INVERSE MATRICES – MATRIX EQUATIONS

4.3 SYSTEMS OF LINEAR EQUATIONS WITH NON-UNIQUE SOLUTIONS

4.4 SYSTEMS OF LINEAR INEQUALITIES

4.5 LINEAR PROGRAMMING , GRAPHICAL METHODS

4.6 MARKOV CHAINS

                       

CHAPTER 5 . EXPONENTIAL AND LOGARITHM

5.1 EXPONENTIAL FUNCTIONS

5.2 LOGARITHMIC FUNCTIONS

5.3 SOLVING EXPONENTIAL EQUATIONS – LOGARITHMIC EQUATIONS

5.4 EXPONENTIAL AND LOGARITHMIC MODELS

                       

CHAPTER 6 . CALCULUS

6.1 SEQUENCES - DISCRETE FUNCTIONS

6.2 SERIES

6.3 LIMITS OF FUNTIONS

6.4 THE DERIVATIVE

6.5 THE INTEGRATION

                       

CHAPTER 7 . APPLICATIONS OF DERIVATIVES AND INTEGRATIONS

7.1 APPLICATIONS OF DERIVATIVES

7.2 APPLICATIONS OF DERIVATIVES ( cont )

7.3 APPLICATIONS OF INTEGRATIONS

7.4 APPLICATIONS OF INTEGRATIONS (cont)

Assignments

There are 5 home assignments based on the topics in chapters above . 

HOME ASSIGNMENT 1

1. LOGIC , SET , COUNTING 

2. PROBABILITY , STATISTICS 

HOME ASSIGNMENT 2

1. FINANCE
2 .GEOMETRY

HOME ASSIGNMENT 3

1. GEOMETRY

2. LINEAR ALGEBRA

HOME ASSIGNMENT 4

1. EXPONENTIAL AND LOGARITHM

2. CALCULUS

HOME ASSIGNMENT 5

1.  LIMITS

2 . DERIVATIVE

3.  INTEGRATION 

Examinations

The midterm and final test are open-book examinations and 1 ½  hours long both . The midterm covers chapters 1 – 4 , and final covers chapters 5 – 7 .

Grading

The final grade will be determined as follows 

TOTAL HOME ASSIGNS SCORES  30% 
MIDTERM SCORES 35%
FINAL SCORES  35%

FINAL
SCORES		GRADES
	0	F
	60	C-
	64	C
	71	C+
	75	B-
	79	B
	86	B+
	90	A-
	94	A

  ***************************************************

-----------------------------------------------------------------------------------------------------------

TOÁN THỰC HÀNH  CHƯƠNG 1 .  1.1

Chương 1 .  LOGIC , TẬP HỢP  VÀ  PHÉP ĐẾM .

 

Bài giảng

1.1          TẬP HỢP – PHÉP TOÁN TẬP HỢP .  

         

Chủ đề 

- Tập hợp và tập hợp con  .

- Phép toán tập hợp  .

- Luật  De Morgan .

Ứng dụng

-Xác định bản số tập hợp .

Khái niệm cơ bản

*  Phép toán tập hợp  ( Hợp , Giao , Hiệu  – Phần bù )  .

1.    Tập hợp – tập hợp con .

- Một tập hợp là một bộ sưu tập các đối tượng hoặc sự vật có cùng tính chất . Những đối tượng hoặc sự vật đó gọi là phần tử của tập hợp .

Ví dụ   A = { a , b , c , 1 , 2 , x , y }

- Bản số của tập hợp  A  là số phần tử của A ký hiệu là card(A)  hoặc  n(A) .

Ví dụ   A = { a , b , c , 1 , 2 , x , y }    ,  n(A)  =  7

- Tập hợp có thể được biểu diễn bởi giản đồ Venn như sau ( Venn diagram  ) 

Ví dụ  . * Lập đội điền kinh .   

Có 148 sinh viên tham gia tập luyện thể dục thể thao trong đó có 76 người thích chạy bộ , 112 người thích nhảy sào và 28 người không thích cả hai bộ môn này . Hỏi số sinh viên vừa thích cả hai môn này là bao nhiêu người để từ đó lập ra một đội tuyển thi đấu điền kinh .


Lời giải .

Gọi tổng số sinh viên tập luyện thể thao là  n(T)  =  148 người 
Số sinh viên thích chạy bộ là  n(B)  =  76 người 
Số sinh viên thích nhảy sào là  n(S)  =   112 người 
Số sinh viên không thích chạy bộ và nhảy sào là  n(~BUS)  =  28 người 
Tập hợp những nsinh viên thích cả hai môn ký hiệu là  B^S .
 
Vậy số người thích chạy bộ hoặc nhảy sào hoặc cả hai môn này là 

n(BUS)   =  n(T)  \  n(~BUS)  =  148  -  28  =  120 ( người )


n(BUS)  =  n(B)  +  n(S)  -  n(B^S)


hay  120  =  76  +  112  -   n(B^S)
Khi đó   n(B^S)   =   76  +  112  -  120  =  68 ( người )






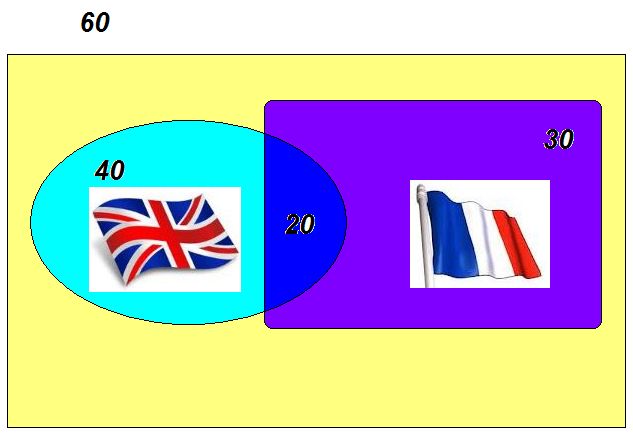
Ví dụ  . * Lựa chọn ngoại ngữ .

Khoa quản trị có 60 sinh viên trong đó có 40 chọn ngoại ngữ Anh , 30 chọn ngoại ngữ Pháp và 20 người chọn cả hai bộ môn này . 

Hỏi số sinh viên 
a. Chỉ chọn ngoại ngữ Anh .
b. Chỉ chọn ngoại ngữ Pháp .
c. Không chọn cả hai ngoại ngữ Anh và Pháp . 
d. Chọn một trong hai  hoặc cả hai ngoại ngữ .


Lời giải .

Lời giải .


Gọi tổng số sinh viên của khoa là  n(K)  =  60
Số sinh viên chọn Anh văn là  n(A)  =  40 người 
Số sinh viên chọn Pháp văn là  n(P)  =  30 người 
Số sinh viên chọn cả hai Anh văn và Pháp văn là n(A^P)  =  20 người .


a. Như vậy số sinh viên chỉ chọn Anh văn là :  n(A~P)  =  40  -  20  =  20 (người)

b. Số sinh viên chỉ chọn Pháp văn là :  n(P~A)  =  30  -  20  =  10 (người)
Như vậy  n(AUP)  =  n(A\P)  +   n(P)  =  ( 40 - 20 ) + 30  = 50 (người)

c. Số sinh viên không chọn cả hai ngoại ngữ là 
n(~A^~P) =  n(K)  -  n(AUP)  =  60  -  50  =  10 ( người)

d. Số sinh viên chọn một trong hai  hoặc cả hai ngoại ngữ là 
n(AUP)  =  50 (người)




*************************************************

Trần hồng Cơ 

20/6/2012



This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

 -------------------------------------------------------------------------------------------
Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.
Pure mathematics is, in its way, the poetry of logical ideas.

Albert Einstein .