VẬT LÝ TỔNG QUAN Chương 1. CƠ HỌC . 1.1 ĐỘNG HỌC . 1.1.2 Khoảng cách - Dịch chuyển

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

VẬT LÝ TỔNG QUAN 

Chương 1. CƠ HỌC .

1.1  ĐỘNG HỌC .

1.1.2   Khoảng cách - Dịch chuyển 


Khái niệm 


Khoảng cách là độ đo của một khoảng giữa hai địa điểm. (Đây không phải là định nghĩa chính thức)  .
Từ "khoảng cách" là câu trả lời cho câu hỏi, "Từ đây đến đó hay giữa đây và đó xa bao nhiêu ?"
Độ đo này có thể là chiều dài , đơn vị biểu diễn chiều dài , hoặc thời gian .

Ví dụ : khoảng cách tính bằng đơn vị biểu diễn độ dài

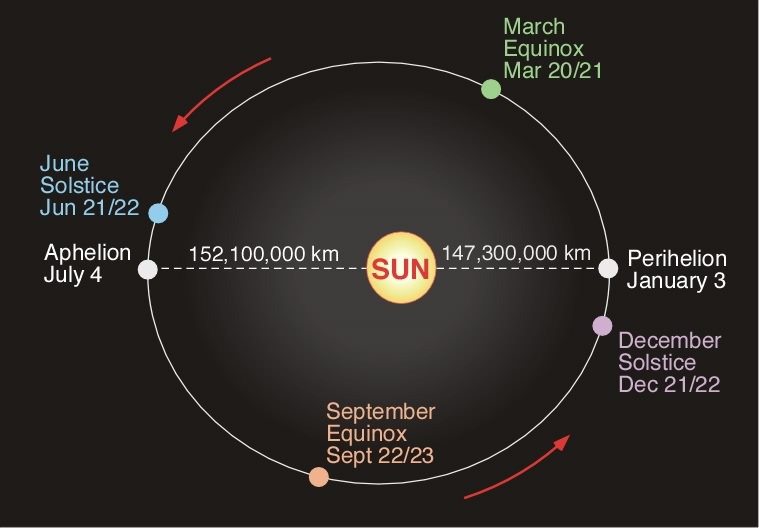
Ví dụ : khoảng cách tính bằng đơn vị thời gian

Lưu ý :
Khoảng cách là một độ đo vô hướng giữa hai địa điểm cần đo dọc theo con đường thực tế kết nối chúng . Khoảng cách này có thể không phải là ngắn nhất .

Hãy xét ví dụ cụ thể như sau : Khoảng cách giữa điểm A thuộc xã Hòa Hưng , huyện Cái Bè , tỉnh Tiền Giang và điểm B thuộc xã Tân Hòa Bắc , thành phố Vĩnh Long gồm các đoạn :
- Từ A đến chân cầu dẫn phía Tiền Giang : 200m
- Toàn bộ chiều dài cầu Mỹ Thuận : 1535m
- Từ chân cầu dẫn phía Vĩnh Long đến vòng xoay : 600m
- Từ vòng xoay phía Vĩnh Long đến B : 1240m
Do đó khoảng cách từ A đến B là : 200m + 1535m + 600m + 1240m  = 3575m .
Ta thường viết là AB = 3575

Dịch chuyển ( chuyển vị ) là khoảng cách ngắn nhất giữa 2 vị trí được nối với nhau theo đoạn thẳng . Nói cách khác là độ đo (module) của vector tạo bởi hai điểm dọc theo con đường ngắn nhất nối chúng .
Như vậy dịch chuyển có 3 yếu tố :
- Phương ( giá )
- Hướng ( chiều ) .
- Độ lớn ( module ).
Quy ước : Tương tự như hệ trục tọa độ Descartes
Dấu (+)  :  Hướng lên trên , sang phải , hướng bắc , hướng đông .
Dấu (-)  :  Hướng xuống dưới , sang trái , hướng nam , hướng tây .

Trong ví dụ ở trên dịch chuyển từ A đến B thực tế là 1408m , ký hiệu  $||\overrightarrow{AB}|| = 1408$
Hình động sau mô tả khoảng cách và dịch chuyển

Ví dụ này cho thấy khoảng cách và sự dịch chuyển có cùng kích thước chỉ khi chúng ta xem xét ở các khoảng nhỏ. Khi dịch chuyển được đo dọc theo con đường ngắn nhất giữa hai điểm, độ lớn của nó là luôn luôn nhỏ hơn hoặc bằng với khoảng cách. Nhưng thế nào là nhỏ? Câu trả lời là, "Nhỏ có tính phụ thuộc tương đối".

Không có quy tắc rốt ráo và nhanh chóng nào có thể được sử dụng để phân biệt lớn và nhỏ. Vi khuẩn là một phân tử lớn, nhưng bạn vẫn không thể nhìn thấy nó nếu không có sự trợ giúp của một kính hiển vi. Tương tự như vậy , chiếc laptop là nhỏ, nhưng bạn không thể bỏ vào trong túi áo sơ-mi của bạn.

Những gì là nhỏ trong bối cảnh này có thể là lớn trong một bối cảnh khác . Vì thế phép tính vi-tích phân đã phát triển để giải quyết các khái niệm về sự nhỏ bé thông qua việc sử dụng các khái niệm giới hạn. Theo ngôn ngữ của phép tính vi-tích phân , độ lớn của dịch chuyển tiến gần đến khoảng cách khi khoảng cách dần về 0 .





Ký hiệu .

Cuối cùng nhưng không kém phần quan trọng là các ký hiệu. Làm thế nào chúng ta phân biệt được khoảng cách và dịch chuyển trong văn bản khoa học . Một số người sử dụng ký hiệu này và một số người khác thì không , hơn nữa cách sử dụng lại không thống nhất . Mặc dù đã có một số mức độ chuẩn hóa trong vật lý, khi nói đến khoảng cách và dịch chuyển, nhưng có vẻ như không ai đồng ý.

Trong các phần dưới đây chúng ta sử dụng các ký hiệu khoảng cách và dịch chuyển tương ứng là s và r .
Tại một điểm A ban đầu và điểm B lúc sau trong hệ trục Oxy được biểu diễn bởi $r_{0}$ và $r$ .
Khi đó dịch chuyển $AB = ||\overrightarrow{AB}|| = || \Delta r || $
Nếu điểm A có khoảng cách ban đầu là $s_{0}$ chuyển động trên đường cong đến vị trí điểm B tương ứng $s_{0}$ thì khoảng cách $AB =  \Delta  s$

Các tính chất của khoảng cách và dịch chuyển .

1 ,  $ ||\Delta r||\leq  \Delta s $

2.   $\Delta s\rightarrow 0\Rightarrow \Delta s\rightarrow ||\Delta r|| $

3. Khoảng cách và dịch chuyển không thay đổi qua phép tịnh tiến .

Tại mọi vị tri khi thực hiện phép tịnh tiến khoảng cách và dịch chuyển đều như nhau . Đây là tính thuần nhất của không gian .

4. Khoảng cách và dịch chuyển không thay đổi qua phép quay .

Tại mọi vị tri khi thực hiện phép quay một góc $\theta$ khoảng cách và dịch chuyển đều như nhau . Đây là tính đẳng hướng của không gian .

5. Khoảng cách và dịch chuyển không thay đổi qua phép đối xứng trục và đối xứng tâm  .

Đối xứng trục 

Đối xứng tâm

Tại mọi vị tri khi thực hiện phép đối xứng trục (tâm)  khoảng cách và dịch chuyển đều như nhau . Đây là tính trực hình của không gian .

Đơn vị 

Đơn vị quốc tê SI về khoảng cách và dịch chuyển là mét (m)  .  Ban đầu mét được xác định là  $1/10^7$ của khoảng cách từ xích đạo đến bắc cực khi được đo đi qua Paris (vì thế chu vi của trái đất sẽ là 40 triệu mét); mét cũng là chiều dài của một thanh kim loại cắt chính xác lưu giữ trong một kho lưu trữ ở ngoại ô Paris; sau đó mét được tính thông qua một số lượng nhất định các bước sóng của một loại  ánh sáng đặc biệt  . Mét hiện nay được xác định theo tốc độ của ánh sáng. Một mét là khoảng cách mà ánh sáng (hoặc bất kỳ bức xạ điện từ khác có bước sóng tùy ý ) truyền qua chân không sau 1 / 299.792.458 giây.
Bội số và ước số thường dùng của mét là kilomet (km)  = $10^3 m $  và centimet (cm)  = $1/10^2 m$

Ngoài ra còn có một số đơn vị tự nhiên được sử dụng trong hàng hải , thiên văn học và khoa học không gian. Một hải lý hiện tại là 1.852 m (6.080 feet), nhưng ban đầu được xác định là một phút của cung trên đường tròn , hay 1/60 của 1/360  chu vi của trái đất. Sau đó mỗi sáu mươi hải lý là một vĩ độ ở bất cứ đâu trên trái đất hoặc một kinh độ trên đường xích đạo.

Khoảng cách trong không gian đôi khi được so sánh với các bán kính của trái đất : $6.4 x 10^6  m$. Một số ví dụ:  Bán kính hành tinh sao Hỏa có khoảng ½ bán kính của trái đất, kích thước của một quỹ đạo địa tĩnh là khoảng 6,5 lần bán kính trái đất, và trái đất cách mặt trăng khoảng 60 lần bán kính trái đất .

Khoảng cách trung bình từ trái đất đến mặt trời được gọi là một đơn vị thiên văn AU : khoảng $1.5 × 10^11  m$ . Khoảng cách từ mặt trời đến sao Hỏa (Mars) là 1.5 AU; từ mặt trời đến Mộc tinh (Jupiter) là 5.2 AU; và từ mặt trời đến Diêm vương tinh (Pluto) là 40 AU. Các ngôi sao gần nhất của mặt trời, chòm sao Nhân Mã (Proxima Centauri)  là khoảng 270.000 AU .

Đối với khoảng cách thực lớn, các nhà thiên văn đưa ra cách tính theo năm ánh sáng . Một năm ánh sáng là khoảng cách ánh sáng đi được trong chân không sau một năm. Nó tương đương với chín nghìn triệu triệu mét (sáu nghìn tỉ dặm). Đơn vị này sẽ được mô tả chi tiết hơn trong các phần tiếp theo .

Câu hỏi

1.   Một chùm tia laser được bắn đi từ một nguồn hợp với trục ngang một góc 15 độ 55' . Sau khi truyền đi được 11520m , tia laser này chạm phải một gương chắn và truyền đi tiếp 8580m với góc lệch là 11 độ 28' rồi chạm đích . Tính dịch chuyển của tia laser và góc lệch của tia so với trục ngang .

2.  Một vận động viên A chạy bộ cách cao ốc thứ nhất B là 1500m , cao ốc B này có chiều cao 120m , thấp hơn chiều của tòa tháp C là 78m . Khoảng cách từ cao ốc B đến tòa tháp C là 1000m . Giả sử A , B' và C' đều nằm trên cùng trục ngang . Hãy tính độ dịch chuyển AC và góc nhìn từ A đến C .

3. Một đường ống dẫn gas có 3 đoạn chính : AB , BC và CD có độ dài lần lượt là 5m , 3.5m và 2.6m . Hãy tính chuyển vị AD và góc lệch giữa AD và trục ngang .

Trần hồng Cơ 
Biên soạn 
Ngày 24/10/2014



Nguồn :
1. http://tap.iop.org/mechanics/kinematics/index.html
2. http://hyperphysics.phy-astr.gsu.edu/hbase/HFrame.html
3. http://physics.info/
4. http://www.onlinephys.com/index.html
5. http://www.stmary.ws/highschool/physics/home/notes/kinematics/




  
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

-------------------------------------------------------------------------------------------

 Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic.

 Pure mathematics is, in its way, the poetry of logical ideas.

 Albert Einstein .