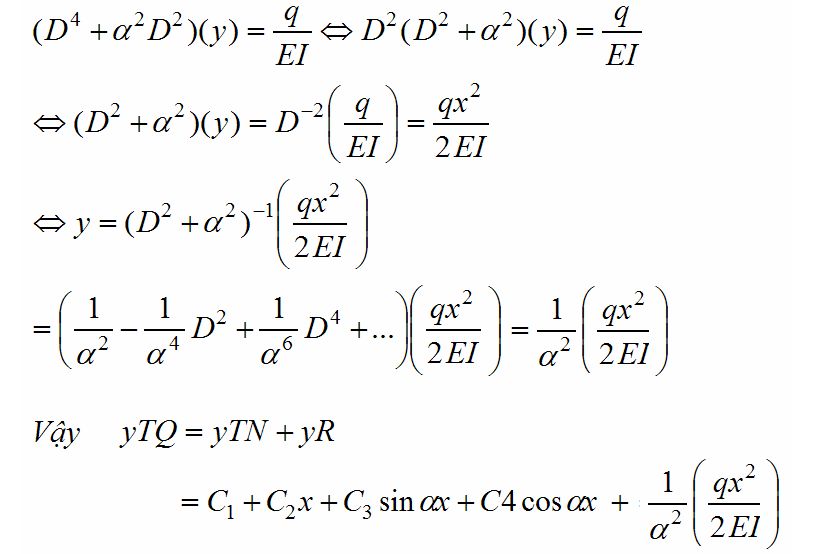GIỚI THIỆU VỀ PHƯƠNG TRÌNH VI PHÂN . Chương 4- PHẦN 2 .

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

   

GIỚI THIỆU VỀ PHƯƠNG TRÌNH VI PHÂN .

Chương 4-

PHẦN 2 . 

Toán tử vi phân ngược .  
Phương pháp toán tử vi phân ngược .
Mô hình ứng dụng .
Bài tập thực hành .  

Loạt bài sau đây giới thiệu về phương trình vi phân một cách tổng quan , các khái niệm cơ bản và phương pháp giải được trình bày tinh giản dễ hiểu . Bạn đọc có thể sử dụng các phần mềm hoặc công cụ online trích dẫn chi tiết trong bài viết này để hỗ trợ cho việc học tập và nghiên cứu . Ngoài ra tác giả cũng sẽ đề cập đến những ví dụ minh họa cụ thể , các mô hình thực tế có ứng dụng trong lĩnh vực phương trình vi phân .  



Trần hồng Cơ .
01/05/2013 .


****************************************************************************


This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

1. Toán tử vi phân ngược .
1.1 Định nghĩa - Các công thức  .


Trong Chương 2-Phần 4 chúng ta đã đề cập đến toán tử vi phân ngược và ứng dụng của nó tìm nghiệm riêng cho phương trình vi phân tuyến tính cấp 2 hệ số hằng . 
Phần nội dung sau đây sẽ bổ sung các công thức , mô tả cách tìm nghiệm riêng của phương trình vi phân tuyến tính cấp cao hệ số hằng bằng phương pháp này qua các ví dụ chi tiết .


1.1.1 Định nghĩa .

*Xem Chương 2-Phần 4  . 1.3.2 
 Xét phương trình vi phân viết dạng toán tử 

** Toán tử vi phân ngược cấp k

1.1.2  Các công thức . 


* Xét phương trình vi phân viết dạng toán tử  

1.2   Định lý bổ sung . 


* Xét phương trình vi phân tuyến tính hệ số hằng dạng 
                          P(D)(y)  =  f    (1)
Với đa thức toán tử 
    

1.2.1   Định lý  . 

Các tính chất phân phối và giao hoán của toán tử vi phân ngược 

Lưu ý :
+Trong phương trình (1) đa thức toán tử  P(D) và hàm f(x) đã cho là duy nhất , nhưng giá trị của toán tử vi phân ngược trên  f(x) có thể là không duy nhất . 
+ Sự sai khác giữa 2 kết quả chính là nghiệm  của phương trình thuần nhất   P(D)(y)  =  0  (2)  .   


1.2.2   Định lý  . 

Tính chất thay thế và nâng toán tử vi phân bằng một hằng số . 
** Liên hệ giữa toán tử vi phân ngược và hàm mũ .




1.3  Phép tính trên toán tử vi phân và toán tử vi phân ngược  .

Các bài tập sau mô tả phép tính toán tử vi phân và vi phân ngược .


Ví dụ 1 . xem Chương 2-Phần 4 . 2  - 2.1 

Lời giải .
1.

2.

Ví dụ 2 .
Tìm kết quả của các phép tính vi phân ngược sau đây 

Lời giải .

Lấy phần thực của K , ta có Re(K) 

đặt theta = 3x , dùng Maple tính toán , rút gọn và lấy phần ảo , ta có 

LƯU Ý KỸ THUẬT .
+ Để tính nhanh kết quả của các phép tính vi phân ngược cho các hàm chứa { sin(bx) , cos(bx) } thay vì dùng công thức Euler như ví dụ 2 d. trên , ta có thể thay thế $Im(e^{ibx})$ , $Re(e^{ibx})$   bằng $(ib)^2$ vào các toán tử vi phân chẵn vì $(ib)^2=-b^2$ .  
Ví dụ 2d  được tính nhanh như sau đây

2. Phương pháp toán tử vi phân ngược .
Từ các bài tập mô tả trình bày ở phần trên , ta sẽ đưa ra phương pháp toán tử vi phân ngược giải phương trình vi phân tuyến tính cấp cao hệ số hằng  . Có thể tham khảo bài viết ở Chương 2-Phần 4   2.2  về phương pháp này .
 

2.1  Áp dụng toán tử vi phân ngược nhận dạng hàm cơ sở  .
2.1.1  Nhắc lại .
Cho phương trình vi phân tuyến tính cấp n hệ số hằng  

Để giải phương trình cấp cao này ta thực hiện 2 bước .
Bước 1 .  Tìm nghiệm thuần nhất yTN của phương trình 

Bước 2 .  Tìm nghiệm riêng yR  của phương trình cấp cao như sau :
1. Tác động toán tử vi phân ngược cho 2 vế phương trình ( dùng khai triển Taylor cho biểu thức toán tử vi phân ngược ) nhận dạng các hàm cơ sở .
2. Khi có được hệ cơ sở ta biểu diễn yR qua các hàm cơ sở  với các hệ số  chưa biết thay vào phương trình vi phân rồi dùng phương pháp hệ số bất định .

Khi đó nghiệm tổng quát của phương trình là 

yTQ  =  yR  +  yTN


2.1.2  Áp dụng . 
Ví dụ 3 . Giải các phương trình vi phân cấp cao sau đây  

2.2  Giải trực tiếp phương trình vi phân tuyến tính cấp cao .
Bước 1 .  Tìm nghiệm thuần nhất yTN của phương trình .

Bước 2 .  Tìm nghiệm riêng yR  của phương trình cấp cao bằng toán tử vi phân ngược .

Khi đó nghiệm tổng quát của phương trình là 

yTQ  =  yR  +  yTN



Ví dụ 4 . Giải các phương trình vi phân cấp cao sau đây

Lời giải .

Các bạn giải tiếp các bài toán còn lại trong ví dụ trên theo 2 bước đã giới thiệu ở phần lý thuyết.  
3. Mô hình ứng dụng .
Phương trình vi phân tuyến tính cấp cao đã trình bày ở phần trên có ứng dụng rất quan trọng cho việc xây dựng các mô hình tính toán cơ , điện , sinh học ... và nhiều lĩnh vực khác kể cả trong kinh tế , môi trường và xã hội . Chúng ta sẽ điểm qua một số bài toán thực tế sau đây .
3.1  Cơ học .
3.1.1 Bài toán kết cấu có kích thước một chiều .
Phương trình vi phân biểu diễn moment uốn của một dầm (beam) chịu tải trọng phân bố có dạng 

 Trong đó M là moment uốn mang dấu (+) ở thớ trên của thiết diện dầm bị nén ; y là độ võng của dầm mang dấu (+) hướng từ dưới lên trên ; q là cường độ của tải trọng phân bố mang dấu (+) hướng từ dưới lên trên ; E là module đàn hồi ; I là moment quán tính của thiết diện ngang của dầm . Các điều kiện biên xuất hiện tại các đầu x = 0  và x = L .

Gọi P là tải trọng dọc trục , phương trình vi phân biểu diễn độ võng được thiết lập từ 

Hệ dầm -cột được áp dụng rộng rãi trong lĩnh vực xây dựng công trình . Xét bài toán tính độ uốn ngang của tháp nước có tải trọng dọc trục là P mô tả như hình sau

Phương trình vi phân biểu diễn độ uốn ngang là

Điều kiện biên tại các đầu x = 0  (ngàm )  và x = L (tự do) .
+ x = 0  ;  y(0) = 0 ;  y'(0) = 0 .
+ x = L  ;  y"(L) = 0 ;  S(L)  =  0 .
Dạng toán tử của phương trình vi phân :

 Tìm nghiệm thuần nhất bằng Maple  

Giả thiết rằng tải gió q(x) = const , áp dụng phương pháp toán tử vi phân ngược tìm nghiệm riêng  

Tìm các hằng số từ điều kiện , ta có :

Khi đó nghiệm tổng quát của phương trình là  

3.1.2 Bài toán dao động của hệ một bậc tự do .
Phương trình vi phân biểu diễn dao động của hệ một bậc tự do với mô hình sau đây có dạng   

Hệ dao động một bậc tự do có rất nhiều ứng dụng trong thực tế , cụ thể như bộ giảm chấn cho ô tô và xe máy .

Từ phương trình dao động trên ta biến đổi thành 

Tìm nghiệm thuần nhất bằng Maple , ta giả thiết rằng 2 nghiệm đặc trưng m1,2  là thực-rời . 

Tìm nghiệm riêng bằng phương pháp biến thiên tham số , đặt  m1,2  như sau

Thiết lập và giải hệ tìm { u'1,2 } .

Tích phân theo t , ta thu được hệ  { u1,2 } và biểu thức của nghiệm riêng .

Nghiệm tổng quát là   xTQ  =  xR  +  xTN

Để xác định các hằng số ta áp các điều kiện đầu như đã nói ở trên .
Nếu  2 nghiệm đặc trưng m1,2  là phức-rời 

Chi tiết của nghiệm trong những trường hợp khác có thể tìm trong các giáo trình về dao động cơ học .

3.2  Điện học .
3.2.1 Bài toán mạch điện RLC .
a. Xét mạch điện gồm điện trở R , cuộn dây có độ tự cảm L , tụ điện có điện dung C mắc nối tiếp với nguồn điện có hiệu điện thế V(t) và cường độ dòng điện trong mạch là i(t) ( xem hình ) .

Phương trình vi phân biểu diễn của mạch nối tiếp là  

b. Xét mạch điện gồm điện trở R , cuộn dây có độ tự cảm L , tụ điện có điện dung C mắc song song với nguồn điện có hiệu điện thế V(t) và cường độ dòng điện trong mạch là i(t) ( xem hình ) .

Phương trình vi phân biểu diễn của mạch song song là  

-----------------------------------------------------------------
3.2.2 Bộ phận đánh lửa cho động cơ nổ . 
Ta xét một bài toán mạch RLC nối tiếp cho bộ phận đánh lửa trong động cơ nổ với các số liệu sau 

Hãy xác định thời điểm để hiệu điện thế giữa 2 đầu cuộn cảm L đạt giá trị lớn nhất và tính VLmax .

Các điều kiện đầu 
+ t = 0 ,  i(0) = V/R  = 12/4  =  3
+ t = 0 ,  i'(0) = i1(0) = 0 .
Nghiệm iTN thu được là 

Để ý rằng do tính chất của hàm sin nên 

4.  Bài tập thực hành . 
4.1  Giải các phương trình vi phân cấp cao thuần nhất sau đây .

4.2  Giải các phương trình vi phân cấp cao sau đây bằng phương pháp hệ số bất định .

4.3  Giải các phương trình vi phân cấp cao sau đây bằng phương pháp biến thiên tham số . 

4.4  Giải các phương trình vi phân cấp cao sau đây bằng phương pháp toán tử vi phân ngược .

Trần hồng Cơ .
14/05/2013 .

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

 -------------------------------------------------------------------------------------------
 Toán học thuần túy, theo cách của riêng nó, là thi ca của tư duy logic. 
 Pure mathematics is, in its way, the poetry of logical ideas. 
 Albert Einstein .